题目内容
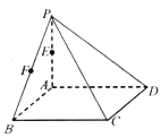
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为平行四边形,其中
为平行四边形,其中![]() ,
,![]() ,
,![]() ,等边
,等边![]() 所在平面与平面
所在平面与平面![]() 垂直.
垂直.
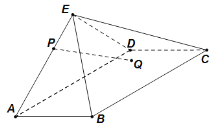
(Ⅰ)点![]() 在棱
在棱![]() 上,且
上,且![]() ,
,![]() 为
为![]() 的重心,求证:
的重心,求证:![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积.
的体积.
【答案】见解析
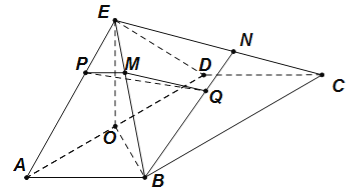
【解析】(Ⅰ)如图,在棱![]() 上取点
上取点![]() ,使得
,使得![]() ;连接
;连接![]() 并延长,交
并延长,交![]() 于点
于点![]() .
.
因为在![]() 中,
中,![]() ,所以
,所以![]() ,
,
又四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,
所以![]() . -----------------2分
. -----------------2分
在![]() 中,
中,![]() 为重心,所以
为重心,所以![]() ,
,
又![]() ,所以
,所以![]() .
.
又![]() ,
,![]() ,
,
所以平面![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() . ---------5分
. ---------5分
(Ⅱ)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
所以![]() 的面积
的面积![]() .--7分
.--7分
取![]() 的中点
的中点![]() ,连结
,连结![]() 、
、![]() .
.
在![]() 中,
中,![]() ,所以
,所以![]() ,且
,且![]() .
.
又因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .--------------10分
.--------------10分
故三棱锥![]() 的体积
的体积![]() .-------12分
.-------12分
【命题意图】本题考查空间中线面平行的证明、几何体体积的求解,考查基本的空间想象能力和逻辑推理能力、运算能力等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目