题目内容
设数列 的前n项和为
的前n项和为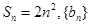 为等比数列,且
为等比数列,且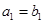 ,
,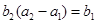 .
.
(1)求数列 和
和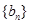 的通项公式;
的通项公式;
(2)设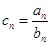 ,求数列
,求数列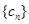 的前n项和
的前n项和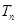 .
.
(1) ,
, ;(2)
;(2) .
.
解析试题分析:解题思路:(1)利用 求
求 ,再利用数列
,再利用数列 的关系求
的关系求 (2)利用错位相减法求和.规律总结:涉及已知
(2)利用错位相减法求和.规律总结:涉及已知 求
求 ,利用
,利用 ,注意验证
,注意验证 时的情况;(2)因为
时的情况;(2)因为 是等差数列,
是等差数列, 是等比数列,则求
是等比数列,则求 的和利用错位相减法.
的和利用错位相减法.
试题解析:(1)当 时,
时, ;
;
当 时,
时, ,也满足上式,所以:
,也满足上式,所以: .
.
又 ,
, ,所以:
,所以: .
.
(2)



所以:



所以: .
.
考点:1.已知 求
求 ;2.错位相减法.
;2.错位相减法.

练习册系列答案
相关题目
 ,当
,当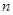 为奇数时,
为奇数时, ;当
;当 ;则
;则 等于 .
等于 . 的前
的前 项和为__________
项和为__________ 中,
中, ,
,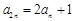 (
( ),
),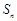 是数列
是数列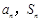 ;
;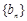 满足
满足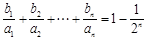 (
( 项和
项和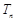 .
.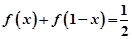 .
.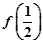 和
和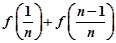 (n∈N*)的值;
(n∈N*)的值; ,求an;
,求an;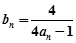 ,
,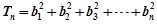 ,
,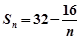 ,试比较Tn和Sn的大小。
,试比较Tn和Sn的大小。 的前
的前 项和为
项和为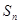 ,对一切正整数
,对一切正整数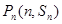 都在函数
都在函数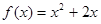 的图象上.
的图象上.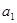 ,
,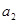 ;
;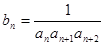 ,求证数列
,求证数列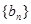 的前
的前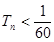 .
.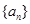 的前
的前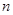 项和为
项和为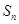 ,
,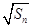 是
是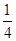 与
与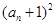 的等比中项.
的等比中项.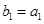 ,且
,且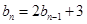 ,求数列
,求数列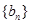 的通项公式;
的通项公式;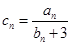 ,求数列
,求数列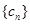 的前
的前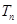 .
.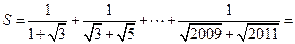 .
.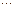 +
+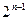 所有项的和为
所有项的和为