题目内容
15.已知函数f(x)=$\left\{\begin{array}{l}x+1\;\;\;(x<0)\\-x-1(x≥0)\end{array}$,则不等式x+(x+1)f(x)≤1的解集是[-3,+∞).分析 分别考虑x<0时;x≥0时的原不等式的解集,最后求并集.
解答 解:当x<0时,f(x)=x+1,则x+(x+1)(x+1)≤1,
x+x2+2x+1≤1,x2+3x≤0,解得-3≤x≤0,
∴-3≤x<0;
当x≥0时,f(x)=-x-1,则x-(x+1)(x+1)≤1,即x2+x+2≥0,恒成立;
∴x≥0
综上所述,原不等式的解集为[-3,+∞);
故答案为:[-3,+∞).
点评 本题考查分段函数的应用,考查分段函数值应考虑自变量对应的情况,属于基础题.

练习册系列答案
相关题目
3.执行如图所示的程序框图,则输出S的值为( )
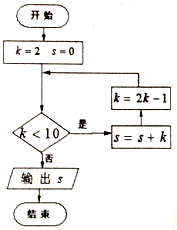

| A. | 10 | B. | 19 | C. | 21 | D. | 36 |
7.已知a>0,x,y满足线性约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≤3}\\{ax-y-3a≤0}\end{array}\right.$,若z=2x+y的最小值为1,则a=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
5.一个盒子里装有相同大小的黑球10个,红球12个,白球4个,从中任取2个,其中白球为X,则下列算式中等于$\frac{{C}_{22}^{1}{C}_{4}^{1}+{C}_{22}^{2}}{{C}_{26}^{2}}$的是( )
| A. | P(0<X≤2) | B. | P(X≤1) | C. | P(X=1) | D. | P(X=2) |
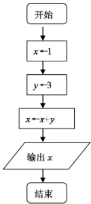 如图所示的算法语句中,输出的结果是x=4.
如图所示的算法语句中,输出的结果是x=4.