题目内容
在△ABC中,已知
•
=9,sinB=cosA•sinC,S△ABC=6,P为线段AB上的一点,且
=x.
+y•
,则
+
的最小值为( )
| AB |
| AC |
| CP |
| ||
|
|
| ||
|
| 1 |
| x |
| 1 |
| y |
A.
| B.
| C.
| D.
|
△ABC中设AB=c,BC=a,AC=b
∵sinB=cosA•sinC∴sin(A+C)=sinCcosnA
即sinAcosC+sinCcosA=sinCcosA
∴sinAcosC=0∵sinA≠0∴cosC=0 C=90°
∵
•
=9,S△ABC=6
∴bccosA=9,
bcsinA=6
∴tanA=
,根据直角三角形可得sinA=
,cosA=
,bc=15
∴c=5,b=3,a=4
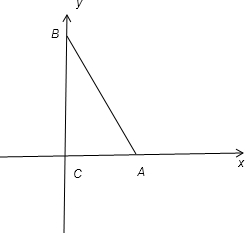
以AC所在的直线为x轴,以BC所在的直线为y轴建立直角坐标系可得C(0,0)A(3,0)B(0,4)
P为线段AB上的一点,则存在实数λ使得
=λ
+(1-λ)
=(3λ,4-4λ)(0≤λ≤1)
设
=
,
=
则|
|=|
|=1,
=(1,0),
=(0,1)
∴
=x
+y
=(x,0)+(0,y)=(x,y)
∴x=3λ,y=4-4λ则4x+3y=12
+
=
(
+
)(4x+3y)=
(7+
+
)≥
+
故所求的最小值为
+
故选:C
∵sinB=cosA•sinC∴sin(A+C)=sinCcosnA
即sinAcosC+sinCcosA=sinCcosA
∴sinAcosC=0∵sinA≠0∴cosC=0 C=90°
∵
| AB |
| AC |
∴bccosA=9,
| 1 |
| 2 |
∴tanA=
| 4 |
| 3 |
| 4 |
| 5 |
| 3 |
| 5 |
∴c=5,b=3,a=4
以AC所在的直线为x轴,以BC所在的直线为y轴建立直角坐标系可得C(0,0)A(3,0)B(0,4)
P为线段AB上的一点,则存在实数λ使得
| CP |
| CA |
| CB |
设
| ||
|
|
| e1 |
| ||
|
|
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
∴
| CP |
| ||
|
|
| ||
|
|
∴x=3λ,y=4-4λ则4x+3y=12
| 1 |
| x |
| 1 |
| y |
| 1 |
| 12 |
| 1 |
| x |
| 1 |
| y |
| 1 |
| 12 |
| 3y |
| x |
| 4x |
| y |
| 7 |
| 12 |
| ||
| 3 |
故所求的最小值为
| 7 |
| 12 |
| ||
| 3 |
故选:C


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
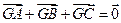 , ②
, ②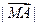 =
= 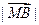 =
= 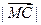 ③
③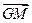 ∥
∥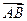
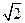 , 0) ,已知
, 0) ,已知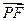 ∥
∥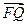 ,
, 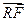 ∥
∥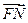 且
且 与
与 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取 和
和 两点,现测得
两点,现测得 ,
, ,
, ,
,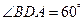 ,
, ,求两景点
,求两景点


 是向量a和b的“向量积”,它的长度
是向量a和b的“向量积”,它的长度 为向量a和b的夹角,若
为向量a和b的夹角,若 = .
= . 是圆
是圆 外一点,直线
外一点,直线 与圆
与圆 、
、 ,
, 、
、 是圆
是圆 、
、 。若
。若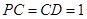 ,则四边形
,则四边形 的面积
的面积 .
.