Question

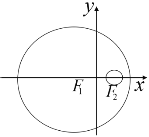
【题目】极坐标系与直角坐标系有相同的长度单位，以原点为极点，以轴正半轴为极轴．已知曲线的极坐标方程为，曲线的极坐标方程为，射线，，，与曲线分别交异于极点的四点，，，．

（）若曲线关于曲线对称，求的值，并把曲线和化成直角坐标方程．

（）求，当时，求的值域．

Answer 1

【答案】（1），，（2）．

【解析】

（1）把、的方程化为直角坐标方程，根据因为曲线关于曲线对称，可得直线x2a＝0经过圆心（1，），求得a＝2，故可得的直角坐标方程；

（2）由题意可得：当α时，|OA|＝4sinα；|OB|＝4cos（α）；|OC|＝4cosα；|OD|＝4sin（α），f（α）＝|OA||OB|+|OC||OD|，利用和差角公式，可得答案．

坐标系与参数方程：（），

即，化为直角坐标方程为．

把的方程化为直角坐标方程为，

因为曲线关于曲线对称，故直线经过圆心，

解得，故的直角坐标方程为．

（）当时，，，

，，

∴

，

的值域为．