题目内容
如图，在平面直角坐标系xOy中，已知曲线C由圆弧C1和圆弧C2相接而成，两相接点M，N均在直线x＝5上．圆弧C1的圆心是坐标原点O，半径为13；圆弧C2过点A(29，0)．
(1)求圆弧C2的方程；
(2)曲线C上是否存在点P，满足PA＝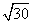
PO？若存在，指出有几个这样的点；若不存在，请说明理由．
解 (1)圆弧C1所在圆的方程为x2＋y2＝169，令x＝5，解得M(5,12)，N(5，－12)．
则线段AM中垂线的方程为y－6＝2(x－17)，令y＝0，得圆弧C2所在圆的圆心为(14,0)，
又圆弧C2所在圆的半径r2＝29－14＝15，
∴圆弧C2的方程为(x－14)2＋y2＝225(5≤x≤29)．
(2)不存在．理由：假设存在这样的点P(x，y)，则由PA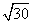＝PO，得x2＋y2＋2x－29＝0，
由
解得x＝－70(舍去)．
由
解得x＝0(舍去)，综上，这样的点P不存在．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
且z＝2x＋y的最大值和最小值分别为m和n，则m－n＝( )
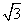，则△AOB的面积S的最小值为( )
B．2
(O为原点)，其中λ1，λ2∈R，且λ1＋λ2＝1，则点C的轨迹是( )