题目内容
在数列{an}中,a1=1, .
.
(1)求an;
(2)设f(x)=sinx,An是数列{f(an)}前n项的和,Bn是{an}前n项的和,比较An与Bn的大小;
解:(1)由 得,nan=(n-1)an-1,(2分)
得,nan=(n-1)an-1,(2分)
∴{nan}构成以1×a1为首项的常数数列,又1×a1=1,故nan=1,∴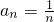 .(5分)
.(5分)
(2)令 ,
,
可使 (x>0).
(x>0).
则在单位圆中,由当
∴ (9分)
(9分)
∴ >0
>0
∴
∴An<Bn.(12分)
分析:(1)化简 ,构造新的数列{nan},求出新数列的通项公式,进而可求出数列的通项公式.
,构造新的数列{nan},求出新数列的通项公式,进而可求出数列的通项公式.
(2)求出{f(an)},利用函数思想创造新的函数 ,求出在任何情况下函数都大于0,即数列{f(an)}得每一项都小于{an}的每一项,进而判断An与Bn的大小.
,求出在任何情况下函数都大于0,即数列{f(an)}得每一项都小于{an}的每一项,进而判断An与Bn的大小.
点评:此题主要考查构造新数列及利用函数思想就绝数列的有关问题.
 得,nan=(n-1)an-1,(2分)
得,nan=(n-1)an-1,(2分)∴{nan}构成以1×a1为首项的常数数列,又1×a1=1,故nan=1,∴
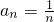 .(5分)
.(5分)(2)令
 ,
,可使
 (x>0).
(x>0).则在单位圆中,由当

∴
 (9分)
(9分)∴
 >0
>0∴

∴An<Bn.(12分)
分析:(1)化简
 ,构造新的数列{nan},求出新数列的通项公式,进而可求出数列的通项公式.
,构造新的数列{nan},求出新数列的通项公式,进而可求出数列的通项公式.(2)求出{f(an)},利用函数思想创造新的函数
 ,求出在任何情况下函数都大于0,即数列{f(an)}得每一项都小于{an}的每一项,进而判断An与Bn的大小.
,求出在任何情况下函数都大于0,即数列{f(an)}得每一项都小于{an}的每一项,进而判断An与Bn的大小.点评:此题主要考查构造新数列及利用函数思想就绝数列的有关问题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 ,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn=
,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn= (n∈N*).
(n∈N*). }的前n项和为Tn,证明:
}的前n项和为Tn,证明: .
.