题目内容
已知函数![]() 的图象经过点
的图象经过点![]() ,
,![]() ,且当
,且当![]() 时,
时,![]() 的最大值是2
的最大值是2![]() -1.
-1.
(1)求![]() 的解析式;
的解析式;
(2)求出满足条件的一个![]() ,使得将
,使得将![]() 的图象按向量
的图象按向量![]() 平移后可以得到一个奇函数的图象.
平移后可以得到一个奇函数的图象.
解:(1)由题意知 ∴b= a =1-c,
∴b= a =1-c,
∴f(x)= c +![]() (1-c)sin(2x+
(1-c)sin(2x+![]() ). ∵x∈[0,
). ∵x∈[0, ![]() ], ∴2x+
], ∴2x+![]() ∈[
∈[![]() ,
,![]() ].
].
当1-c>0时, 由c +![]() (1-c)=2
(1-c)=2![]() -1, 解得c =-1;
-1, 解得c =-1;
当1-c<0时, c +![]() (1-c)?
(1-c)?![]() =2
=2![]() -1, 无解;
-1, 无解;
当1-c =0时,c =2![]() -1,相矛盾. 综上可知c =-1.
-1,相矛盾. 综上可知c =-1.
∴f(x)= 2![]() sin(2x+
sin(2x+![]() )-1.
)-1.
(2)∵g(x)=2![]() sin2x是奇函数,将g(x)的图象向左平移
sin2x是奇函数,将g(x)的图象向左平移![]() 个单位,再向下平移一个单位就可以得到f(x)的图象.
个单位,再向下平移一个单位就可以得到f(x)的图象.
因此,将f(x)的图象向右平移![]() 个单位,再向上平移一个单位就可以得到奇函数g(x)=2
个单位,再向上平移一个单位就可以得到奇函数g(x)=2![]() sin2x的图象.
sin2x的图象.
故![]() =(
=(![]() ,1)是满足条件的一个向量.
,1)是满足条件的一个向量.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的图象经过点
的图象经过点 和
和 ,记
,记
 的通项公式;
的通项公式; ,若
,若 ,求
,求 的最小值;
的最小值; 对一切
对一切 均成立的最大实数
均成立的最大实数 .
.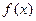 的图象经过点
的图象经过点 ,且对任意
,且对任意 ,都有
,都有 数列
数列 满足
满足
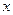 为正整数时,求
为正整数时,求 的表达式
的表达式 ,求
,求
 ,总有
,总有 ,求实数
,求实数 的取值范围
的取值范围 的图象经过点M(1,4),曲线在点M处的切线恰好与直线
的图象经过点M(1,4),曲线在点M处的切线恰好与直线 垂直。
垂直。 的值;
的值; 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围.
的取值范围. 的图象经过点
的图象经过点 ,则该函数的一条对称轴
,则该函数的一条对称轴 B.
B. C.
C. D.
D.
 的图象经过点
的图象经过点 和原点,则
和原点,则 .
.