题目内容
已知函数 的图象经过点M(1,4),曲线在点M处的切线恰好与直线
的图象经过点M(1,4),曲线在点M处的切线恰好与直线 垂直。
垂直。
(1)求实数 的值;
的值;
(2)若函数 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.
【答案】
(1) ;(2)
;(2)
【解析】
试题分析:(1)
∵曲线在点M(1,4)出的切线恰好与直线 垂直
垂直
∴ ①
①
又 的图像经过M(1,4)
的图像经过M(1,4)
∴ ②
②
联立①②解得
(2)由(1)得 则
则

令 解得
解得
∴ 在
在 上为增函数
上为增函数
∴ 即
即
考点:导数的几何意义,直线方程,应用导数研究函数的单调性。
点评:中档题,在给定区间,导数非负,函数为增函数,导数非正,函数为减函数。涉及函数单调性及参数范围的讨论问题,往往通过研究函数的单调性,最值等,得以解答。两直线垂直,斜率乘积为-1.

练习册系列答案
相关题目
 的图象经过点
的图象经过点 和
和 ,记
,记
 的通项公式;
的通项公式; ,若
,若 ,求
,求 的最小值;
的最小值; 对一切
对一切 均成立的最大实数
均成立的最大实数 .
.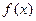 的图象经过点
的图象经过点 ,且对任意
,且对任意 ,都有
,都有 数列
数列 满足
满足
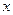 为正整数时,求
为正整数时,求 的表达式
的表达式 ,求
,求
 ,总有
,总有 ,求实数
,求实数 的取值范围
的取值范围 的图象经过点
的图象经过点 ,则该函数的一条对称轴
,则该函数的一条对称轴 B.
B. C.
C. D.
D.
 的图象经过点
的图象经过点 和原点,则
和原点,则 .
.