题目内容
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求证数列![]() 中不存在任意三项按原来顺序成等差数列;
中不存在任意三项按原来顺序成等差数列;
(3)若从数列![]() 中依次抽取一个无限多项的等比数列,使它的所有项和
中依次抽取一个无限多项的等比数列,使它的所有项和![]() 满足
满足![]() ,这样的等比数列有多少个?
,这样的等比数列有多少个?
解:(1)当![]() 时,
时,![]() ,则
,则![]() .
.
又![]() ,
,![]() ,两式相减得
,两式相减得![]() ,
,
![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列,
的等比数列, ![]() -----------4分
-----------4分
(2)反证法:假设存在三项按原来顺序成等差数列,记为![]()
则![]() ,
,![]() (*)又
(*)又![]()
![]()
![]() *式左边是偶数,右边是奇数,等式不成立
*式左边是偶数,右边是奇数,等式不成立
![]() 假设不成立 原命题得证. -------------8分
假设不成立 原命题得证. -------------8分
(3)设抽取的等比数列首项为![]() ,公比为
,公比为![]() ,项数为
,项数为![]() ,
,


练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,满足
,满足 .
. 为等比数列,并
为等比数列,并 求出
求出 ;
; ,求
,求 的最大项.
的最大项. }的前
}的前 项和为
项和为 ,且
,且 (
( );
); =3
=3 (
(


 ;
; }的通项公式
}的通项公式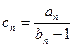 ,求数列
,求数列 的前
的前 .
. 的前
的前 项和为
项和为 ,且
,且 .
.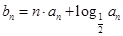 ,数列
,数列 的前
的前 ,若不等式
,若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.