ĖâÄŋÄÚČŨ
ŌŅÖĒČįÍŧŖŦÖąĪßlŖēx=-
Ŗ¨pŖž0ŖŠŖŦĩãF(
ŖŦ0)ŖŦPÎĒÆŊÃæÉĪĩÄļ¯ĩãŖŦšũP×÷ÖąĪßlĩÄ´šĪßŖŦ´š×ãÎĒĩãQŖŦĮŌ
•
=
•
ŖŽ
Ŗ¨1ŖŠĮķļ¯ĩãPĩÄšėŧŖCĩġŊŗĖŖģ
Ŗ¨2ŖŠĩąp=2ĘąŖŦĮúĪßCÉĪ´æÔÚ˛ģÍŦĩÄÁŊĩãšØĶÚÖąĪßy=kx+3ļÔŗÆŖŦĮķĘĩĘũkÂú×ãĩÄĖõŧūŖ¨Đ´ŗöšØĪĩĘŊŧ´ŋÉŖŠŖģ
Ŗ¨3ŖŠÉčļ¯ĩãM Ŗ¨aŖŦ0ŖŠŖŦšũMĮŌĐąÂĘÎĒ1ĩÄÖąĪßĶëšėŧŖCŊģĶÚ˛ģÍŦĩÄÁŊĩãAŖŦBŖŦĪßļÎABĩÄÖĐ´šĪßĶëxÖáŊģĶÚĩãNŖŦĩą|AB|ĄÜ2pĘąŖŦĮķĄ÷NABÃæģũĩÄ×î´ķÖĩŖŽ
| p |
| 2 |
| p |
| 2 |
| QP |
| QF |
| FP |
| FQ |
Ŗ¨1ŖŠĮķļ¯ĩãPĩÄšėŧŖCĩġŊŗĖŖģ
Ŗ¨2ŖŠĩąp=2ĘąŖŦĮúĪßCÉĪ´æÔÚ˛ģÍŦĩÄÁŊĩãšØĶÚÖąĪßy=kx+3ļÔŗÆŖŦĮķĘĩĘũkÂú×ãĩÄĖõŧūŖ¨Đ´ŗöšØĪĩĘŊŧ´ŋÉŖŠŖģ
Ŗ¨3ŖŠÉčļ¯ĩãM Ŗ¨aŖŦ0ŖŠŖŦšũMĮŌĐąÂĘÎĒ1ĩÄÖąĪßĶëšėŧŖCŊģĶÚ˛ģÍŦĩÄÁŊĩãAŖŦBŖŦĪßļÎABĩÄÖĐ´šĪßĶëxÖáŊģĶÚĩãNŖŦĩą|AB|ĄÜ2pĘąŖŦĮķĄ÷NABÃæģũĩÄ×î´ķÖĩŖŽ
Ŗ¨1ŖŠÉčĩãP×øąęÎĒPŖ¨xŖŦyŖŠŖŦÔōĩãQ×øąęÎĒQŖ¨-
ŖŦy)
Ôō
=(x+
ŖŦ0)ŖŦ
=(pŖŦ-y)ŖŦ
=(x-
ŖŦy)ŖŦ
=(-pŖŦy)Ŗ¨2ˇÖŖŠ
ĶÉ
•
=
•
ŖŽĩÃŖēy2=2pxŖ¨pŖž0ŖŠŖ¨4ˇÖŖŠ
Ŗ¨2ŖŠp=2ĘąŖŦy2=4xŖŽ
ÉčĮúĪßCÉĪšØĶÚÖąĪßy=kx+3ļÔŗÆĩãÎĒAŖ¨x1ŖŦy1ŖŠŖŦBŖ¨x2ŖŦy2ŖŠŖŦ
ÔōÖąĪßABËųÔÚÖąĪߡŊŗĖÎĒx+ky+n=0ŖŦŖ¨nÎĒŗŖĘũŖŠŖŽ
´úČëy2=4xĩÃy2+4ky+4n=0
Ą÷=Ŗ¨4kŖŠ2-16nŖž0ŧ´k2-nŖž0Ŗ¨3ˇÖŖŠ
ĶÖĄßABÖĐĩãMÔÚÖąĪßy=kx+3ÉĪŖŦ
ÔōŖ¨2k2-nŖŦ-2kŖŠ´úČëy=kx+3ĩÃ-2k=2k3-nk+3Ŗ¨5ˇÖŖŠ
Ąā
ŧ´k2+
+2Ŗŧ0ŖŽ Ŗ¨6ˇÖŖŠ
Ŗ¨3ŖŠÁĒÁĸ
?y2-2px-2pa=0ŖŦ
ĄßĄ÷=4p2+8paŖž0?aŖž-
Ŗ¨1ˇÖŖŠ
Ąā|AB|=
|x1-x2|=
|y1-y2|=
ĄÜ2p
ĄāaĄÜ-
Ąā-
ŖŧaĄÜ-
ŖŽ Ŗ¨2ˇÖŖŠ
ABÖĐ´šĪßy-p=-Ŗ¨x-a-pŖŠŖŦŧ´y=-x+a+2p
Áîy=0ŖŦx=a+2p
Ąāh=
=
pŖ¨3ˇÖŖŠ
ĄāSĄ÷=
•
ĄÁ
=P
Ŗ¨4ˇÖŖŠ
ÔÚ(-
ĩĨĩ÷ĩŨÔö Ŗ¨5ˇÖŖŠ
ĩąa=-
ĘąŖŦSmax=
p2ŖŽ Ŗ¨6ˇÖŖŠ
| p |
| 2 |
Ôō
| QP |
| p |
| 2 |
| QF |
| FP |
| p |
| 2 |
| FQ |
ĶÉ
| QP |
| QF |
| FP |
| FQ |
Ŗ¨2ŖŠp=2ĘąŖŦy2=4xŖŽ
ÉčĮúĪßCÉĪšØĶÚÖąĪßy=kx+3ļÔŗÆĩãÎĒAŖ¨x1ŖŦy1ŖŠŖŦBŖ¨x2ŖŦy2ŖŠŖŦ
ÔōÖąĪßABËųÔÚÖąĪߡŊŗĖÎĒx+ky+n=0ŖŦŖ¨nÎĒŗŖĘũŖŠŖŽ
´úČëy2=4xĩÃy2+4ky+4n=0
Ą÷=Ŗ¨4kŖŠ2-16nŖž0ŧ´k2-nŖž0Ŗ¨3ˇÖŖŠ
ĶÖĄßABÖĐĩãMÔÚÖąĪßy=kx+3ÉĪŖŦ
ÔōŖ¨2k2-nŖŦ-2kŖŠ´úČëy=kx+3ĩÃ-2k=2k3-nk+3Ŗ¨5ˇÖŖŠ
Ąā
|
ŧ´k2+
| 3 |
| k |
Ŗ¨3ŖŠÁĒÁĸ
|
ĄßĄ÷=4p2+8paŖž0?aŖž-
| p |
| 2 |
Ąā|AB|=
| 2 |
| 2 |
| 2 |
| (2p)2+8pa |
ĄāaĄÜ-
| p |
| 4 |
Ąā-
| p |
| 2 |
| p |
| 4 |
ABÖĐ´šĪßy-p=-Ŗ¨x-a-pŖŠŖŦŧ´y=-x+a+2p
Áîy=0ŖŦx=a+2p
Ąāh=
| |2p| | ||
|
| 2 |
ĄāSĄ÷=
| 2p |
| 2 |
| (2p)2+8pa |
| 1 |
| 2 |
| 4p2+8pa |
ÔÚ(-
| p |
| 2 |
ĩąa=-
| p |
| 4 |
| 2 |

ÁˇĪ°˛áĪĩÁĐ´đ°¸
ĪāšØĖâÄŋ
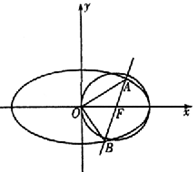 ČįÍŧŖŦÍÖÔ˛GĩÄÖĐĐÄÔÚ×øąęÔĩãŖŦÆäÖĐŌģ¸öŊšĩãÎĒÔ˛FŖēx2+y2-2x=0ĩÄÔ˛ĐÄŖŦĶŌļĨĩãĘĮÔ˛FĶëxÖáĩÄŌģ¸öŊģĩãŖŽŌŅÖĒÍÖÔ˛GĶëÖąĪßlŖēx-my-1=0ĪāŊģĶÚAĄĸBÁŊĩãŖŽ
ČįÍŧŖŦÍÖÔ˛GĩÄÖĐĐÄÔÚ×øąęÔĩãŖŦÆäÖĐŌģ¸öŊšĩãÎĒÔ˛FŖēx2+y2-2x=0ĩÄÔ˛ĐÄŖŦĶŌļĨĩãĘĮÔ˛FĶëxÖáĩÄŌģ¸öŊģĩãŖŽŌŅÖĒÍÖÔ˛GĶëÖąĪßlŖēx-my-1=0ĪāŊģĶÚAĄĸBÁŊĩãŖŽ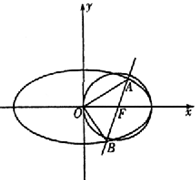 ČįÍŧŖŦÍÖÔ˛GĩÄÖĐĐÄÔÚ×øąęÔĩãŖŦÆäÖĐŌģ¸öŊšĩãÎĒÔ˛FŖēx2+y2-2x=0ĩÄÔ˛ĐÄŖŦĶŌļĨĩãĘĮÔ˛FĶëxÖáĩÄŌģ¸öŊģĩãŖŽŌŅÖĒÍÖÔ˛GĶëÖąĪßlŖēx-my-1=0ĪāŊģĶÚAĄĸBÁŊĩãŖŽ
ČįÍŧŖŦÍÖÔ˛GĩÄÖĐĐÄÔÚ×øąęÔĩãŖŦÆäÖĐŌģ¸öŊšĩãÎĒÔ˛FŖēx2+y2-2x=0ĩÄÔ˛ĐÄŖŦĶŌļĨĩãĘĮÔ˛FĶëxÖáĩÄŌģ¸öŊģĩãŖŽŌŅÖĒÍÖÔ˛GĶëÖąĪßlŖēx-my-1=0ĪāŊģĶÚAĄĸBÁŊĩãŖŽ