题目内容
已知f(x)=2x-
(1)当a∈R,求f(x)在[-2,2]的最小值;
(2)当a=1,2tf(2t)-mf(t)+2-t≥0恒成立,求m的取值范围.
| a |
| 2x |
(1)当a∈R,求f(x)在[-2,2]的最小值;
(2)当a=1,2tf(2t)-mf(t)+2-t≥0恒成立,求m的取值范围.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)令2x=t,由x∈[-2,2],可得t∈[
,4].令g(t)=f(x)=t-
.t∈[
,4].通过对a分类讨论,利用导数研究其单调性即可;
(2)当a=1,2tf(2t)-mf(t)+2-t≥0化为m(4t-1)≤42t,通过对t分类讨论,利用基本不等式的性质即可得出.
| 1 |
| 4 |
| a |
| t |
| 1 |
| 4 |
(2)当a=1,2tf(2t)-mf(t)+2-t≥0化为m(4t-1)≤42t,通过对t分类讨论,利用基本不等式的性质即可得出.
解答:
解:(1)令2x=t,∵x∈[-2,2],∴2x∈[
,4],即t∈[
,4].
令g(t)=f(x)=t-
.t∈[
,4].
则g′(t)=1+
.
当a≥0时,g′(t)>0,∴函数g(t)在t∈[
,4]单调递增,∴当t=
时,g(t)取得最小值,且g(
)=
-4a.
当a<0时,g′(t)=
=
,
①当
≥4时,即a≤-16时,g′(t)≤0,函数g(t)在t∈[
,4]上单调递减,∴当t=4时,函数g(t)取得最小值,g(4)=4-
.
②当
≤
时,即-
≤a<0时,g′(t)≥0,函数g(t)在t∈[
,4]上单调递增,∴当t=
时,函数g(t)取得最小值,g(
)=
-4a.
③当
<
<4时,即-16<a<-
时,当
≤t<
时,g′(t)<0,此时函数g(t)单调递减;当
<t≤4时,g′(t)>0,此时函数g(t)单调递增.
∴当t=
时,函数g(t)取得最小值,g(
)=2
.
综上可得:f(x)min=
.
(2)当a=1,2tf(2t)-mf(t)+2-t≥0化为m(4t-1)≤42t,
当t=0时,对于任意实数m恒成立;
当t<0时,4t<1,上式化为m≥
,∵
=
=4t-1+
+2=-[(1-4t)+
]+2<0,可得m≥0.
当t>0时,4t>1,上式化为m≤
,∵
=
=4t-1+
+2≥2
+2=4,当且仅当t=
时取等号,可得m≤4.
综上可得:0≤m≤4.
即m的取值范围是:[0,4].
| 1 |
| 4 |
| 1 |
| 4 |
令g(t)=f(x)=t-
| a |
| t |
| 1 |
| 4 |
则g′(t)=1+
| a |
| t2 |
当a≥0时,g′(t)>0,∴函数g(t)在t∈[
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
当a<0时,g′(t)=
| t2+a |
| t2 |
(t+
| ||||
| t2 |
①当
| -a |
| 1 |
| 4 |
| a |
| 4 |
②当
| -a |
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
③当
| 1 |
| 4 |
| -a |
| 1 |
| 16 |
| 1 |
| 4 |
| -a |
| -a |
∴当t=
| -a |
| -a |
| -a |
综上可得:f(x)min=
|
(2)当a=1,2tf(2t)-mf(t)+2-t≥0化为m(4t-1)≤42t,
当t=0时,对于任意实数m恒成立;
当t<0时,4t<1,上式化为m≥
| 42t |
| 4t-1 |
| 42t |
| 4t-1 |
| 42t-1+1 |
| 4t-1 |
| 1 |
| 4t-1 |
| 1 |
| 1-4t |
当t>0时,4t>1,上式化为m≤
| 42t |
| 4t-1 |
| 42t |
| 4t-1 |
| 42t-1+1 |
| 4t-1 |
| 1 |
| 4t-1 |
(4t-1)•
|
| 1 |
| 2 |
综上可得:0≤m≤4.
即m的取值范围是:[0,4].
点评:本题考查了利用导数研究函数的单调性极值与最值、基本不等式的性质,考查了分类讨论的思想方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
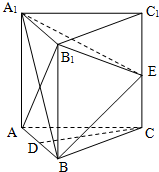 如图,在三棱柱ABC-A1B1C1中,每个侧面均为边长为2的正方形,D为底边AB的中点,E为侧棱CC1的中点.
如图,在三棱柱ABC-A1B1C1中,每个侧面均为边长为2的正方形,D为底边AB的中点,E为侧棱CC1的中点.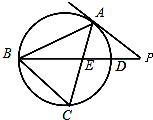 如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,∠ABC=60°,PD=1,BD=8,则BC=
如图,△ABC是⊙O的内接三角形,PA是⊙O的切线,PB交AC于点E,交⊙O于点D,若PE=PA,∠ABC=60°,PD=1,BD=8,则BC=