题目内容

关于平面向量
a
，
b
，
c
，有下列三个命题：
①若
a
•
b
=
a
•
c
，则
b
=
c
、
②若
a
=（1，k），
b
=（-2，6），
a
∥
b
，则k=-3．
③非零向量
a
和
b
满足|
a
|=|
b
|=|
a
-
b
|，则
a
与
a
+
b
的夹角为60°．
其中真命题的序号为
 
．（写出所有真命题的序号）
分析：①向量不满足约分运算，但满足分配律，由此我们利用向量的运算性质，可判断平面向量
a
，
b
，
c
的关系；
②中，由
a
∥
b
，我们根据两个向量平行，坐标交叉相乘差为0的原则，可以构造一个关于k的方程，解方程即可求出k值；
③中，若|
a
|=|
b
|=|
a
-
b
|，我们利用向量加减法的平行四边形法则，可以画出满足条件图象，利用图象易得到两个向量的夹角；
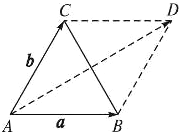解答：精英家教网解：①若
a
•
b
=
a
•
c
，则
a
•（
b
-
c
）=0，此时
a
⊥（
b
-
c
），而不一定
b
=
c
，①为假．
②由两向量
a
∥
b
的充要条件，知1×6-k•（-2）=0，解得k=-3，②为真．
③如图，在△ABC中，设
AB
=a，
AC
=b，
CB
=a-b，
由|
a
|=|
b
|=|
a
-
b
|，可知△ABC为等边三角形．
由平行四边形法则作出向量
a
+
b
=
AD
，
此时
a
与
a
+
b
成的角为30°．③为假．
综上，只有②是真命题．
答案：②
点评：本题考查的知识点是向量的运算性质及命题的真假判断与应用，处理的关键是熟练掌握向量的运算性质，如两个向量垂直，则数量积为0，两个向量平等，坐标交叉相乘差为0等．
练习册系列答案
相关题目
关于平面向量
a
，
b
，
c
，有下列命题：
①（
a
•
b
）
c
-（
c
•
a
）
b
=0
②|
a
|-|
b
|＜|
a
-
b
|；
③（
b
•
c
）
a
-（
c
•
a
）
b
不与
c
垂直；
④非零向量
a
和
b
满足|
a
|=|
b
|=|
a
-
b
|，则
a
与
a
-
b
的夹角为60°．
其中真命题的个数为（　　）
A、1个B、2个C、3个D、4个
关于平面向量
a
，
b
，
c
，有下列四个命题（　　）
①若
a
∥
b
，
.
a
≠
0
则?λ∈R，使得
b
=λ
a

②
.
a
•
.
b
=0，则
a
=
o
或
b
=
0

③若
.
a
=(1，k)，
b
=(-2，6)，
.
a
∥
b
则，k=-3
④若
a
•
b
=
a
•
c
 则
a
⊥(
b
-
c
)，其中正确命题序号是（　　）
关于平面向量
a
，
b
，
c
．有下列三个命题：
①若
a
•
b
=
a
•
c
，则
b
=
c
；
②若
a
=(1，k)，
b
=(-2，6)，
a
∥
b
，则k=-3；
③非零向量
a
和
b
满足|
a
|=|
b
|=|
a
-
b
|，则
a
与
a
+
b
的夹角为30°．
其中真命题的序号为
②③
②③
．（写出所有真命题的序号）
关于平面向量
a
，
b
，
c
．有下列三个命题：
①若
a
•
b
=
a
•
c
，则
b
=
c
．
②若
a
=（1，k），
b
=（-2，6），
a
∥
b
，则k=-3．
③非零向量
a
和
b
满足|
a
|=|
b
|=|
a
-
b
|，则
a
与
a
+
b
的夹角为60°．
其中真命题的个数有（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网