题目内容
已知| OA |
| a |
| OB |
| b， |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
分析：由于本题中未给出向量的坐标，故求向量的模时，主要是根据向量数量的数量积计算公式，求出向量模的平方，即向量的平方，再开方求解．求出模后，根据向量数量积计算公式的变形，求出两向量夹角的余弦值．
解答：解：∵|
+
|2=(
+
)2=
2+
2+2
•
由|
|=|
|=2，∠AOB=60°，得：
2=
2= 4，
•
=2
∴|
+
|2=12，∴|
+
|=2
令
+
与
的夹角为θ
则0≤θ≤π，且cosθ=
=
∴θ=
故答案为：2
，
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
由|
| a |
| b |
| a |
| b |
| a |
| b |
∴|
| a |
| b |
| a |
| b |
| 3 |
令
| a |
| b |
| b |
则0≤θ≤π，且cosθ=
| ||||||
|
|
| ||
| 2 |
∴θ=
| π |
| 6 |
故答案为：2
| 3 |
| π |
| 6 |
点评：求向量的模一般有两种情况：若已知向量的坐标，或向量起点和终点的坐标，则
=
或|
|=
；若未知向量的坐标，只是已知条件中有向量的模及夹角，则求向量的模时，主要是根据向量数量的数量积计算公式，求出向量模的平方，即向量的平方，再开方求解．
| a |
| x2+y2 |
| AB |
| (x1-x2)2+(y1-y2)2 |
练习册系列答案
阅读快车系列答案
相关题目
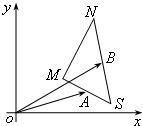如图，已知