题目内容
(本小题14分)
(I)已知数列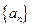 满足
满足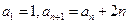
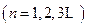 ,
,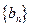 满足
满足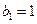 ,
,
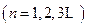 ,求证:
,求证: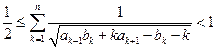 。.
。.
(II) 已知数列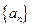 满足:a
满足:a =1且
=1且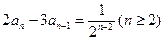 。设m
。设m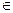 N
N ,m
,m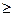 n
n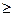 2,证明(a
2,证明(a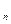 +
+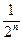 )
)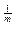 (m-n+1)
(m-n+1)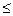
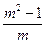

(I)已知数列
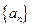 满足
满足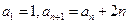
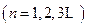 ,
,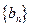 满足
满足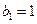 ,
,
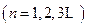 ,求证:
,求证: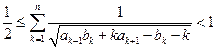 。.
。.(II) 已知数列
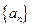 满足:a
满足:a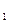 =1且
=1且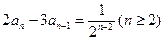 。设m
。设m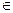 N
N ,m
,m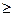 n
n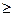 2,证明(a
2,证明(a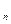 +
+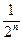 )
)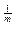 (m-n+1)
(m-n+1)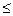
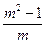

证明:
(I)记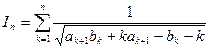 ,则
,则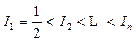 。 …… 2分
。 …… 2分
而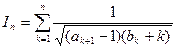
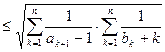 。 ……………… 4分
。 ……………… 4分
因为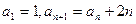 ,所以
,所以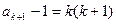 。 ………………… 5分
。 ………………… 5分
从而有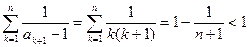 。 ①
。 ①
又因为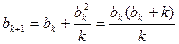 ,所以
,所以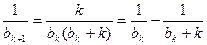 ,
,
即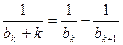 。从而有
。从而有 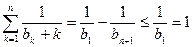 。② … 6分
。② … 6分
由(1)和(2)即得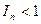 。综合得到
。综合得到 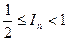 。
。
左边不等式的等号成立当且仅当 n=1时成立。 ……… 7分
(II)不妨设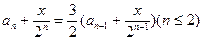 即
即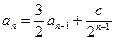 与
与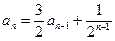 比较系数得c=1.即
比较系数得c=1.即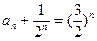
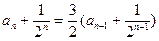
又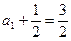 ,故{
,故{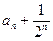 }是首项为
}是首项为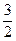 公比为
公比为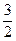 的等比数列,
的等比数列,
故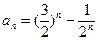 ……… 10分
……… 10分
这一问是数列、二项式定理及不等式证明的综合问题.综合性较强.
即证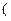
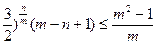 ,当m=n时显然成立。易验证当且仅当m=n=2时,等号成立。
,当m=n时显然成立。易验证当且仅当m=n=2时,等号成立。
设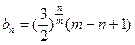 下面先研究其单调性。当
下面先研究其单调性。当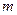 >n时,
>n时,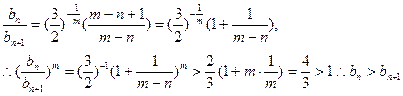 ……… 12分
……… 12分
即数列{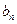 }是递减数列.因为n
}是递减数列.因为n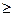 2,故只须证
2,故只须证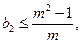 即证
即证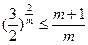 。事实上,
。事实上,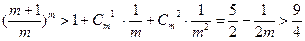 故上不等式成立。综上,原不等式成立。 ……………… 14分
故上不等式成立。综上,原不等式成立。 ……………… 14分
(I)记
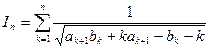 ,则
,则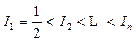 。 …… 2分
。 …… 2分而
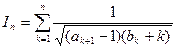
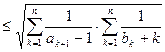 。 ……………… 4分
。 ……………… 4分因为
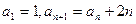 ,所以
,所以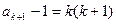 。 ………………… 5分
。 ………………… 5分从而有
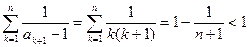 。 ①
。 ①又因为
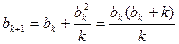 ,所以
,所以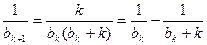 ,
,即
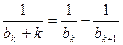 。从而有
。从而有 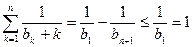 。② … 6分
。② … 6分由(1)和(2)即得
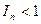 。综合得到
。综合得到 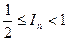 。
。左边不等式的等号成立当且仅当 n=1时成立。 ……… 7分
(II)不妨设
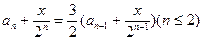 即
即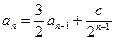 与
与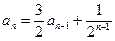 比较系数得c=1.即
比较系数得c=1.即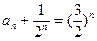
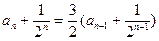
又
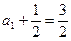 ,故{
,故{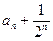 }是首项为
}是首项为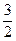 公比为
公比为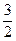 的等比数列,
的等比数列,故
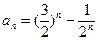 ……… 10分
……… 10分这一问是数列、二项式定理及不等式证明的综合问题.综合性较强.
即证
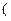
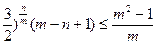 ,当m=n时显然成立。易验证当且仅当m=n=2时,等号成立。
,当m=n时显然成立。易验证当且仅当m=n=2时,等号成立。设
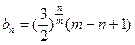 下面先研究其单调性。当
下面先研究其单调性。当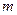 >n时,
>n时,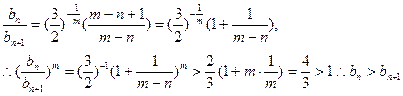 ……… 12分
……… 12分即数列{
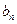 }是递减数列.因为n
}是递减数列.因为n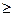 2,故只须证
2,故只须证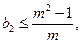 即证
即证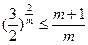 。事实上,
。事实上,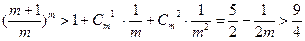 故上不等式成立。综上,原不等式成立。 ……………… 14分
故上不等式成立。综上,原不等式成立。 ……………… 14分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,规定
,规定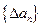 为数列
为数列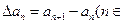 N*).对正整数k,规定
N*).对正整数k,规定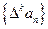 为
为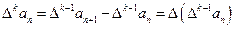 .
.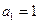 ,且满足
,且满足 ,求数列
,求数列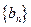 是等差数列,使得
是等差数列,使得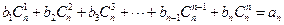 对一切正整数
对一切正整数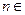 N*都成立,求
N*都成立,求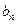 ;
;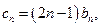 设
设 若
若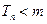 成立,求最小正整数
成立,求最小正整数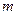 的值.
的值.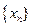 的前n项和为
的前n项和为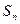 满足
满足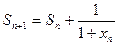 ,
,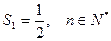
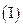 猜想数列
猜想数列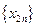 的单调性,并证明你的结论;
的单调性,并证明你的结论;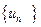 若存在常数M>0,对任意的
若存在常数M>0,对任意的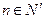 ,恒有
,恒有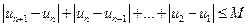 ,, 则称数列
,, 则称数列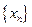 是B-数列吗? 并证明你的结论。
是B-数列吗? 并证明你的结论。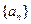 中,
中,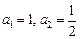 ,
,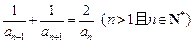 ,
,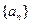 中,各项都是正数,且
中,各项都是正数,且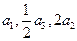 成等差数列,则
成等差数列,则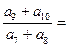
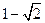
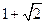
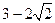
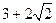
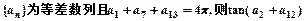 的值为 ( )
的值为 ( )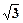
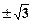
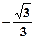
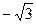
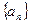 满足
满足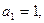
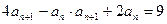
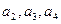 ;
;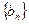 满足
满足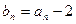 ,猜想数列
,猜想数列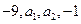
 四个实数成等差数列,
四个实数成等差数列,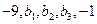 五个实数成等比数列,则
五个实数成等比数列,则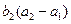 的值等于
的值等于 


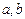 满足:
满足: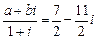 (其中
(其中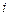 是虚数单位),若用
是虚数单位),若用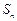 表示数列
表示数列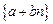 的前
的前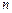 项的和,则
项的和,则