题目内容
已知函数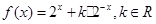 .
.
(I)若函数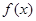 为奇函数,求实数
为奇函数,求实数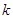 的值;
的值;
(II)若对任意的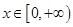 ,都有
,都有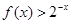 成立,求实数
成立,求实数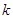 的取值范围.
的取值范围.
【答案】
(I) (II)
(II)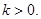
【解析】
试题分析:(Ⅰ)根据 是奇函数,得到恒等式
是奇函数,得到恒等式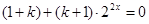 ,对一切
,对一切 恒成立,即得.
恒成立,即得.
(Ⅱ)由 均有
均有 ,即
,即 成立,
成立,
转化成 对
对 恒成立,即所以
恒成立,即所以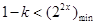 .只需求
.只需求 在
在 的最小值.
的最小值.
试题解析:(Ⅰ)因为 是奇函数,所以
是奇函数,所以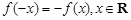 ,
,
即 所以
所以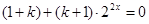 ,对一切
,对一切 恒成立,
恒成立,
所以 4分
4分
(Ⅱ)因为 均有
均有 ,即
,即 成立,
成立,
所以 对
对 恒成立,
8分
恒成立,
8分
所以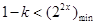 .
.
因为 在
在 上单调递增,所以
上单调递增,所以
所以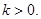 12分
12分
考点:函数的奇偶性,函数的单调性、最值.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 .
. 的单调区间;
的单调区间; 的图象在点(2,f(2))处的切线的倾斜角为45o,对于任意的t
的图象在点(2,f(2))处的切线的倾斜角为45o,对于任意的t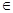 [1,2],函数
[1,2],函数 是
是
 .
. ,求函数
,求函数 极值;ww..com
极值;ww..com
 ,若函数F(x)在[0,1]上单调递增,求
,若函数F(x)在[0,1]上单调递增,求 的取值范围.
的取值范围. .
. 在点
在点 处的切线斜率为4,求实数
处的切线斜率为4,求实数 的值;
的值; 在区间
在区间 上存在零点,求实数
上存在零点,求实数
 ,求
,求 的单调区间;
的单调区间; 在
在 单调增加,在
单调增加,在 单调减少,
单调减少, <6.
<6.