题目内容
(本小题满分10分)选修4—5:不等式选讲已知函数
(1)当 时,求
时,求 的解集;
的解集;
(2)若关于 的不等式
的不等式 的解集是
的解集是 ,求
,求 的取值范围.
的取值范围.

(1)当
 时,求
时,求 的解集;
的解集;(2)若关于
 的不等式
的不等式 的解集是
的解集是 ,求
,求 的取值范围.
的取值范围.(1)  . (2)
. (2) .
.
 . (2)
. (2) .
. (1)先利用零点分段法去掉绝对值转化为分段函数,然后分段求解,再求并集即可.
(2)本小题实质是恒成立问题,即求出f(x)的最小值,令最小值大于或等于2得到关于m的不等式,求出m的取值范围.
解:(1)
 ,
, 
 . 令
. 令
 .
.
则不等式等价于 或
或 或
或 ,
,
解之得 或
或 ,
, 不等式的解集为
不等式的解集为 .
.  5分
5分
(2)
 ,
,
 .
.
由题意,不等式 的解集是
的解集是 ,
,
则 在
在 上恒成立.
上恒成立.
而 , 故
, 故 . 10分
. 10分
(2)本小题实质是恒成立问题,即求出f(x)的最小值,令最小值大于或等于2得到关于m的不等式,求出m的取值范围.
解:(1)

 ,
, 
 . 令
. 令 .
.则不等式等价于
 或
或 或
或 ,
,解之得
 或
或 ,
, 不等式的解集为
不等式的解集为 .
.  5分
5分(2)

 ,
,
 .
.由题意,不等式
 的解集是
的解集是 ,
,则
 在
在 上恒成立.
上恒成立.而
 , 故
, 故 . 10分
. 10分
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目

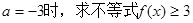 的解集
的解集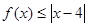 的解集包含[1,2],求
的解集包含[1,2],求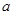 的取值范围
的取值范围 的不等式
的不等式 的解集为非空集合,求实数
的解集为非空集合,求实数 的取值范围。
的取值范围。 的解集为__
的解集为__ 
 的解集非空, 则实数
的解集非空, 则实数 的取值范围是
的取值范围是



 对任意的实数
对任意的实数 恒成立,则实数
恒成立,则实数 的取值范围为
的取值范围为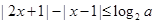 (其中
(其中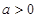 )。
)。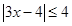 的解集是
的解集是