题目内容
16.定义域为R的函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}|x-1|,x≠1}\\{1,x=1}\end{array}\right.$,若关于x的方程f2(x)+bf(x)+c=0恰有3个不同的实数解x1,x2,x3,则f(x1+x2+x3)等于( )| A. | 0 | B. | 1 | C. | 3lg2 | D. | 3log23 |
分析 作函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}|x-1|,x≠1}\\{1,x=1}\end{array}\right.$的图象,从而可得f(x)=1,从而解得x1+x2+x3=3,从而解得.
解答 解:作函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}|x-1|,x≠1}\\{1,x=1}\end{array}\right.$的图象如下,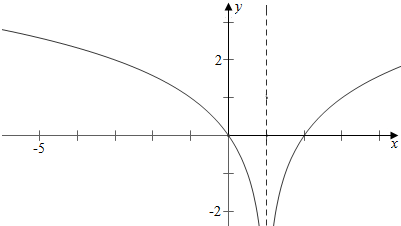 ,
,
∵关于x的方程f2(x)+bf(x)+c=0恰有3个不同的实数解x1,x2,x3,
∴f(x)=1,
结合图象可知,
x1+x2+x3=3,
故f(x1+x2+x3)=f(3)=log2|3-1|=1,
故选:B.
点评 本题考查了数形结合的思想应用及方程的解与函数的图象的关系应用.

练习册系列答案
相关题目
4.某单位有840名职工,现采用系统抽样方法,抽取42人做问卷调查,将840人从1到840进行编号,求得间隔数k=$\frac{840}{42}$=20,即每20人抽取一个人,其中21号被抽到,则抽取的42人中,编号落入区间[421,720]的人数为( )
| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
6.A、B、C、D.E、F共6人站成一排照相,要求A不站在两侧,而且B、C两人站在一起,那么不同的站法种数为( )
| A. | 72 | B. | 96 | C. | 144 | D. | 288 |
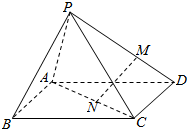 如图,设P为长方形ABCD所在平面外一点,M在PD上,N在AC上,若$\frac{DM}{MP}$=$\frac{CN}{NA}$,用向量法证明:直线MN∥平面PAB.
如图,设P为长方形ABCD所在平面外一点,M在PD上,N在AC上,若$\frac{DM}{MP}$=$\frac{CN}{NA}$,用向量法证明:直线MN∥平面PAB. 一个容量为200的样本频率分布直方图如图所示,则样本数据落在范围[5,9)的频率和频数分别为0.2和180.
一个容量为200的样本频率分布直方图如图所示,则样本数据落在范围[5,9)的频率和频数分别为0.2和180.