题目内容

已知椭圆两焦点三等分椭圆两准线间的距离，则此椭圆的离心率为
 
．
分析：应用两准线间的距离为
2a2
c
，两焦点间的距离2c．
解答：解：两准线间的距离为
2a2
c
，两焦点间的距离2c，
∵两焦点三等分椭圆两准线间的距离，
∴2c=
1
3
•
2a2
c
，即：6c2=2a2，
e=
3
3
，或e=-
3
3
（舍去）
故答案为
3
3
．
点评：本题考查椭圆的几何性质．
练习册系列答案
相关题目
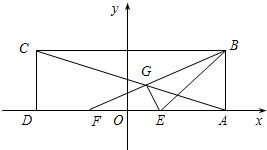精英家教网在矩形ABCD中，已知AD=6，AB=2，E、F为AD的两个三等分点，AC和BF交于点G，△BEG的外接圆为⊙H．以DA所在直线为x轴，以DA中点O为坐标原点，建立如图所示的平面直角坐标系．
（1）求以F、E为焦点，DC和AB所在直线为准线的椭圆的方程．
（2）求⊙H的方程．
（3）设点P（0，b），过点P作直线与⊙H交于M，N两点，若点M恰好是线段PN的中点，求实数b的取值范围．
如图，椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的右焦点是F（1，0），0为坐标原点．
（Ⅰ）已知椭圆短轴的两个三等分点与一个焦点构成正三角形，求椭圆的方程；
（Ⅱ）点M是直线l：x=4上的动点，以OM为直径的圆过点N，且NF⊥OM，是否存在一个定点，使得N到该定点的距离为定值？并说明理由．
已知椭圆短轴上的两个三等分点与两个焦点构成的四边形的周长等于长轴长，则椭圆的离心率为
10
8
10
8
．
（2012•河西区二模）已知双曲线
x2
a2
-
y2
b2
=1（a＞b＞0）的两焦点间的线段F1F2正好被椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的两焦点三等分，则该双曲线的渐近线方程为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网