题目内容
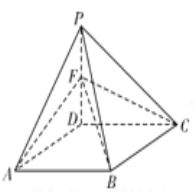
【题目】已知椭圆![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
,![]() 为椭圆
为椭圆![]() 上位于
上位于![]() 轴同侧的两点,
轴同侧的两点,![]() 的周长为
的周长为![]() ,
,![]() 的最大值为
的最大值为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() ,求四边形
,求四边形![]() 面积的取值范围.
面积的取值范围.
【答案】(Ⅰ) ![]() ; (Ⅱ)
; (Ⅱ) ![]()
【解析】
(Ⅰ)由题意得2a+2c=6,即a+c=3,再由当A为椭圆C的上下顶点时,∠F1AF2的最大值为![]() ,此时△AF1F2为等边三角形,得a=2c,结合隐含条件联立解得a,b的值,则可求椭圆方程;
,此时△AF1F2为等边三角形,得a=2c,结合隐含条件联立解得a,b的值,则可求椭圆方程;
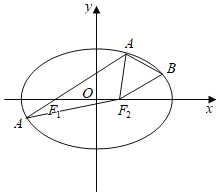
(Ⅱ)由![]() ,得
,得![]() ,延长
,延长![]() 交椭圆C于点
交椭圆C于点![]() ,由(Ⅰ)知
,由(Ⅰ)知![]() ,
,![]() ,设
,设![]() ,
,![]() ,联立直线方程与椭圆方程,化为关于y的一元二次方程,利用根与系数的关系及弦长公式求得四边形
,联立直线方程与椭圆方程,化为关于y的一元二次方程,利用根与系数的关系及弦长公式求得四边形![]() 的面积S,再由换元法及函数的单调性求解.
的面积S,再由换元法及函数的单调性求解.
(Ⅰ)![]() 的周长为
的周长为![]() ,
,![]() ,即
,即![]() .①
.①
当![]() 为椭圆
为椭圆![]() 的上下顶点时,
的上下顶点时,![]() 最大为
最大为![]() ,此时
,此时![]() 为等边三角形,
为等边三角形,![]() .②
.②
由①②及![]() ,解得
,解得![]() ,
,![]() ,
,![]() ,
,
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() ;
;
(Ⅱ)![]() ,
,![]() ,延长
,延长![]() 交椭圆
交椭圆![]() 于点
于点![]() ,
,
由(Ⅰ)知![]() ,
,![]() ,设
,设![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
联立方程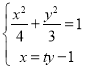 ,消去
,消去![]() 并整理得
并整理得![]() ,
,
![]() ,
,![]() ,设
,设![]() 与
与![]() 的距离为
的距离为![]() ,
,
则四边形![]() 面积
面积![]() ,
,
![]() ,
,
令![]() ,则
,则![]()
![]() ,
,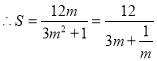 ,
,![]() 函数
函数![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,故四边形
,故四边形![]() 面积的取值范围是
面积的取值范围是![]() .
.

【题目】某地1~10岁男童年龄![]() (单位:岁)与身高的中位数
(单位:岁)与身高的中位数![]() (单位
(单位![]() ,如表所示:
,如表所示:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 76.5 | 88.5 | 96.8 | 104.1 | 111.3 | 117.7 | 124 | 130 | 135.4 | 140.2 |
对上表的数据作初步处理,得到下面的散点图及一些统计量的值.
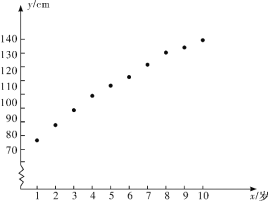
|
|
|
|
112.45 | 82.50 | 3947.71 | 566.85 |
(1)求![]() 关于
关于![]() 的线性回归方程(回归方程系数精确到0.01);
的线性回归方程(回归方程系数精确到0.01);
(2)某同学认为方程![]() 更适合作为
更适合作为![]() 关于
关于![]() 的回归方程模型,他求得的回归方程是
的回归方程模型,他求得的回归方程是![]() .经调查,该地11岁男童身高的中位数为
.经调查,该地11岁男童身高的中位数为![]() ,与(1)中的线性回归方程比较,哪个回归方程的拟合效果更好?
,与(1)中的线性回归方程比较,哪个回归方程的拟合效果更好?
(3)从6岁~10岁男童中每个年龄阶段各挑选一位男童参加表演(假设该年龄段身高的中位数就是该男童的身高).再从这5位男童中任挑选两人表演“二重唱”,则“二重唱”男童身高满足![]() 的概率是多少?
的概率是多少?
参考公式: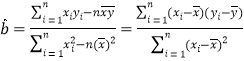 ,
,![]()