Question

【题目】椭圆的左、右焦点分别为，为椭圆上一动点（异于左、右顶点），若的周长为，且面积的最大值为.

（1）求椭圆的方程；

（2）设是椭圆上两动点，线段的中点为，的斜率分别为 为坐标原点，且，求的取值范围.

Answer 1

【答案】（1）；（2）.

【解析】

（1）通过2a+2c=且，计算即得结论；

（2）当直线AB的斜率k＝0时，|OP|，

当直线AB的斜率k≠0时，可令AB的方程为：x＝my+t，由可得（m2+4）y2+2mty+t2﹣4＝0，求得p（，）．由，2t2＝m2+4，代入|OP|2的运算中，化简得|OP|2∈（，2]即可．

（1）由题知，的周长为2a+2c=且，

∴，c=

∴椭圆C的方程为：；

（2）当直线AB的斜率k＝0时，

此时k1，k2（O为坐标原点），满足，k1＝-k2=﹣．

可令OB的方程为：y，（xB＞0）

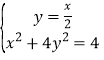由可得B（，），

此时|OP|，

当直线AB的斜率k≠0时，可令AB的方程为：x＝my+t，

由可得（m2+4）y2+2mty+t2﹣4＝0，

△＝4m2t2﹣4（m2+4）（t2﹣4）＞0m2﹣t2+4＞0…①

，

x1+x2＝m（y1+y2）+2t．

∴p（，）．

∵，∵4y1y2+x1x2＝0．

（4+m2）y1y2+mt（y1+y2）+t2＝0．

t2﹣4t2＝0．

2t2＝m2+4，且t2≥2，…②

由①②可得t2≥2恒成立，

|OP|2∈（，2]

|OP|．

综上，|OP|的取值范围为[，]．