题目内容

求证：函数y=xsinx+cosx在区间（
3π
2
，
5π
2
）上是增函数．
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：求出函数的导数，判断函数的导数在区间上的符号，利用导函数的符号，判断函数的单调性即可证明本题．
解答： 证明：函数y=xsinx+cosx，
则函数y′=sinx+xcosx-sinx=xcosx．
∵x∈（
3π
2
，
5π
2
），∴cosx＞0，
∴xcosx＞0，即x∈（
3π
2
，
5π
2
），y′＞0恒成立，
∴函数y=xsinx+cosx在区间（
3π
2
，
5π
2
）上是增函数．
命题成立．
点评：本题考查函数的导数的应用，函数的单调性的判断，考查分析问题解决问题的能力．
练习册系列答案
相关题目
已知函数f（x）=（x+2a）|x-a|+x，a∈R．
（1）当a=0时，判断函数y=f（x）的奇偶性，并加以证明；
（2）若对任意的x∈[-2，2]，函数f（x）图象恒在函数g（x）=（2a+1）x+4a2的图象的下方，求实数a的取值范围．
已知数列{an}的前n项和Sn满足Sn=n2•an（n∈N*），且a1=
1
2
．
（1）求a2，a3，a4的值；
（2）猜想an的表达式（不必证明）．
设a，b是夹角为30°的异面直线，则满足条件“a⊆α，b⊆β，且α⊥β”的平面α，β（　　）
A、不存在B、有且只有一对
C、有且只有两对D、有无数对
已知数列{an}的通项公式an=log2
n+1
n+2
（n∈N*），设数列{an}的前n项的和为Sn，则使Sn＜-5成立的正整数n的最小值为
 
（2）已知命题：“在等差数列{an}中，若4a2+a10+a（）=24，则S11为定值”为真命题，由于印刷问题，括号处的数模糊不清，可推得括号内的数为
 
．
已知抛物线y=
1
4
x2的焦点为F，定点M（1，2），点A为抛物线上的动点，则|AF|+|AM|的最小值为（　　）
A、
3
2
B、
5
2
C、3
D、5
对?x，y∈R，函数f（x）满足f（x+y）=f（x）+f（y）+1，f（1）=a（a为大于0的常数），已知an=f（n）（n∈N*），则下列结论一定正确的是（　　）
A、数列{lgan}为等差数列
B、数列{lgan}为等比数列
C、数列{e an}为等差数列
D、数列{e an}为等比数列
已知函数f（x）=x2+bx+c为偶函数，关于x的方程f（x）=a（x+1）2（a≠1）的根构成集合{1}．
（1）求a，b，c的值；
（2）求证：
f(x)
≤
5
-1
2
|x|+1对任意的x∈[-2，2]恒成立；
（3）设g（x）=
f(x)
+
f(2-x)
若存在x1，x2∈[0，2]，使得|g（x1）-g（x2）|≥m，求实数m的取值范围．
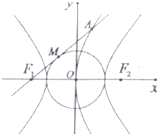如图，双曲线C1：
x2
a2
-
y2
b2
=1，（a＞0，b＞0）的左、右焦点分别为F1，F2，抛物线C2的顶点为坐标原点O，焦点为F2，过F1的直线与抛物线C2的一个交点为A，与圆x2+y2=a2相切于点M，若线段F1A的中点恰为M，则双曲线C1的离心率为（　　）
A、
1+
5
2
B、
1+
3
2
C、
5
2
D、
3+
5
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网