题目内容
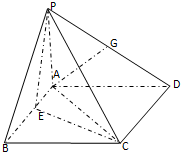 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,A点在PD上的射影为G点,E点在AB上,平面PEC⊥平面PDC.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,A点在PD上的射影为G点,E点在AB上,平面PEC⊥平面PDC.(Ⅰ)求证:AG∥平面PEC;
(Ⅱ)求AE的长;
(Ⅲ)求二面角E-PC-A的正弦值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)通过证明CD⊥平面PAD,AG⊥平面PCD,作EF⊥PC于F,证明EF∥AG,利用直线与平面平行的判定定理证明AG∥平面PEC.
(Ⅱ)证明AE∥平面PCD,推出AE=GF,通过PA2=PG•PD,求出PG,利用
=
求出AE,即可.
(Ⅲ)过E作EO⊥AC于O点,说明∠EFO即为二面角E-PC-A的平面角,利用sin∠EFO=
求出结果即可.
(Ⅱ)证明AE∥平面PCD,推出AE=GF,通过PA2=PG•PD,求出PG,利用
| GF |
| CD |
| PG |
| PD |
(Ⅲ)过E作EO⊥AC于O点,说明∠EFO即为二面角E-PC-A的平面角,利用sin∠EFO=
| EO |
| EF |
解答:
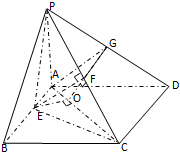 解:(Ⅰ)证明:∵CD⊥AD,CD⊥PA
解:(Ⅰ)证明:∵CD⊥AD,CD⊥PA
∴CD⊥平面PAD∴CD⊥AG,
又PD⊥AG
∴AG⊥平面PCD …(2分)
作EF⊥PC于F,因面PEC⊥面PCD
∴EF⊥平面PCD∴EF∥AG
又AG?面PEC,EF?面PEC,
∴AG∥平面PEC …(4分)
(Ⅱ)由(Ⅰ)知A、E、F、G四点共面,又AE∥CD∴AE∥平面PCD
∴AE∥GF∴四边形AEFG为平行四边形,∴AE=GF …(5分)
∵PA=3,AB=4∴PD=5,AG=
,
又PA2=PG•PD∴PG=
…(6分)
又
=
∴GF=
=
∴AE=
…(8分)
(Ⅲ)过E作EO⊥AC于O点,易知EO⊥平面PAC,
又EF⊥PC,∴OF⊥PC∴∠EFO即为二面角E-PC-A的平面角 …(10分)EO=AE•sin45°=
×
=
,又EF=AG=
∴sin∠EFO=
=
×
=
…(13分)
 解:(Ⅰ)证明:∵CD⊥AD,CD⊥PA
解:(Ⅰ)证明:∵CD⊥AD,CD⊥PA∴CD⊥平面PAD∴CD⊥AG,
又PD⊥AG
∴AG⊥平面PCD …(2分)
作EF⊥PC于F,因面PEC⊥面PCD
∴EF⊥平面PCD∴EF∥AG
又AG?面PEC,EF?面PEC,
∴AG∥平面PEC …(4分)
(Ⅱ)由(Ⅰ)知A、E、F、G四点共面,又AE∥CD∴AE∥平面PCD
∴AE∥GF∴四边形AEFG为平行四边形,∴AE=GF …(5分)
∵PA=3,AB=4∴PD=5,AG=
| 12 |
| 5 |
又PA2=PG•PD∴PG=
| 9 |
| 5 |
又
| GF |
| CD |
| PG |
| PD |
| ||
| 5 |
| 36 |
| 25 |
| 36 |
| 25 |
(Ⅲ)过E作EO⊥AC于O点,易知EO⊥平面PAC,
又EF⊥PC,∴OF⊥PC∴∠EFO即为二面角E-PC-A的平面角 …(10分)EO=AE•sin45°=
| 36 |
| 25 |
| ||
| 2 |
18
| ||
| 25 |
| 12 |
| 5 |
∴sin∠EFO=
| EO |
| EF |
18
| ||
| 25 |
| 5 |
| 12 |
3
| ||
| 10 |
点评:本题考查二面角的平面角的求法,直线与平面垂直与平行的判定定理的应用,考查空间想象能力以及计算能力.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
双曲线
-
=1(a>0,b>0)的离心率是2,则渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、3x±y=0 | ||
B、x±
| ||
| C、x±3y=0 | ||
D、
|
若函数f(x)=x3-mx2+mx+3m在(0,1)内有极大值,无极小值,则( )
| A、m<0 | B、m<3 |
| C、m>3 | D、0<m<3 |
数列{an}中,an=
,则前n和Sn等于( )
| 2 |
| n(n+1) |
A、
| ||
B、
| ||
C、
| ||
D、
|
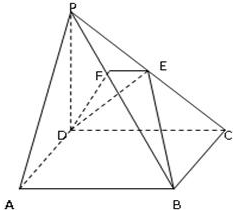 在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ACD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ACD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.