题目内容
已知数列{an}的前n项和为Sn,其中a1=
,5Sn=7an-an-1+5Sn-1(n≥2);等差数列{bn},其中b3=2,b5=6.
(1)求数列{an}的通项公式.
(2)在数列{bn}中是否存在一项bm(m为正整数),使得b3,b5,bm成等比数列,若存在,求m的值;若不存在,说明理由.
(3)若cn=(bn+3)an,求数列{cn}的前n项和Tn.
| 1 |
| 2 |
(1)求数列{an}的通项公式.
(2)在数列{bn}中是否存在一项bm(m为正整数),使得b3,b5,bm成等比数列,若存在,求m的值;若不存在,说明理由.
(3)若cn=(bn+3)an,求数列{cn}的前n项和Tn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)利用等比数列的通项公式即可得出;
(2)利用等差数列与等比数列的通项公式即可得出;
(3)利用“错位相减法”、等比数列的前n项和公式即可得出.
(2)利用等差数列与等比数列的通项公式即可得出;
(3)利用“错位相减法”、等比数列的前n项和公式即可得出.
解答:
解:(1)5Sn-5Sn-1=7an-an-1,
∴2an=an-1,
=
,
∵a1=
,
∴an=
(
)n-1=
.
(2)∵等差数列{bn},b3=2,b5=6,
∴bn=2n-4,
∴bn=2m-4.
假设存在m使得b3,b5,bm成等比数列,
∴b52=b3•bm,
∴m=11,
因此存在m使得b3,b5,bm成等比数列.
(3)cn=(2n-1)×
,
∴
∴
Tn=
+2×(
+
+…+
)-(2n-1)×
=
+
-(2n-1)×
,
∴Tn=3-
.
∴2an=an-1,
| an |
| an-1 |
| 1 |
| 2 |
∵a1=
| 1 |
| 2 |
∴an=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2n |
(2)∵等差数列{bn},b3=2,b5=6,
∴bn=2n-4,
∴bn=2m-4.
假设存在m使得b3,b5,bm成等比数列,
∴b52=b3•bm,
∴m=11,
因此存在m使得b3,b5,bm成等比数列.
(3)cn=(2n-1)×
| 1 |
| 2n |
∴
|
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
2×
| ||||
1-
|
| 1 |
| 2n+1 |
∴Tn=3-
| 2n+3 |
| 2n |
点评:本题考查了等差数列与等比数列的通项公式、“错位相减法”、等比数列的前n项和公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知f(x)=ax2+bx+c,且b>0,若对任意x有f(x)≥0,则
的最小值为( )
| f(1) |
| b |
| A、3 | ||
B、
| ||
| C、2 | ||
D、
|
已知F1(-c,0),F2(c,0)是双曲线C:
-
=1(a>0,b>0)的左右焦点,若p为双曲线右支上一点,满足
•
=4ac,∠F1PF2=
,则该双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
| π |
| 3 |
A、2
| ||||
B、
| ||||
| C、2 | ||||
D、
|
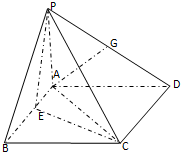 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,A点在PD上的射影为G点,E点在AB上,平面PEC⊥平面PDC.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,A点在PD上的射影为G点,E点在AB上,平面PEC⊥平面PDC.