题目内容

如图，已知椭圆分别为其左右焦点，A为左顶点，直线l的方程为x=4，过F2的直线l′与椭圆交于异于A的P、Q两点．
（Ⅰ）求的取值范围；
（Ⅱ）若求证：M、N两点的纵坐标之积为定值；并求出该定值．
解：（Ⅰ）①当直线PQ的斜率不存在时，
由F2(1,0)可知PQ方程为代入椭圆得
又∴，   
②当直线PQ的斜率存在时，
设PQ方程为代入椭圆得


∴
                  
综上,的取值范围是
（Ⅱ）AP的方程为得
同理,得
∴
1°当k不存在时,=-9 
2°当k存在时, =-9
∴M,N两点的纵坐标之积为定值-9  
练习册系列答案
相关题目
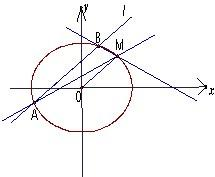精英家教网如图，已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)过点．(1，
2
2
)，离心率为
2
2
，左、右焦点分别为F1、F2．点p为直线l：x+y=2上且不在x轴上的任意一点，直线PF1和PF2与椭圆的交点分别为A、B和C、D，O为坐标原点．
（1）求椭圆的标准方程；
（2）设直线PF1、PF2的斜线分别为k1、k2．①证明：
1
k1
-
3
k2
=2；②问直线l上是否存在点P，使得直线OA、OB、OC、OD的斜率kOA、kOB、kOC、kOD满足kOA+kOB+kOC+kOD=0？若存在，求出所有满足条件的点P的坐标；若不存在，说明理由．
精英家教网如图，已知椭圆C过点M（2，1），两个焦点分别为(-
6
，0)、(
6
，0)，O为坐标原点，平行于OM的直线l交椭圆C于不同的两点A、B，
（Ⅰ）求椭圆C的方程；
（Ⅱ）试问直线MA、MB的斜率之和是否为定值，若为定值，求出以线段AB为直径且过点M的圆的方程；若不存在，说明理由．

(本题满分12分)如图，已知椭圆焦点为，双曲线，设是双曲线上异于顶点的任一点，直线与椭圆的交点分别为和。

（1）   设直线的斜率分别为和，求的值；

（2）   是否存在常数，使得恒成立？若存在，试求出的值；若不存在，请说明理由。

 

 
如图，已知椭圆焦点为F1、F2，双曲线G：x2-y2=4，设P是双曲线G上异于顶点的任一点，直线PF1、PF2与椭圆的交点分别为A、B和C、D．
（1）设直线PF1、PF2的斜率分别为k1和k2，求k1•k2的值；
（2）是否存在常数λ，使得|AB|+|CD|=λ|AB|•|CD|恒成立？若存在，试求出λ的值；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网