题目内容
如图,已知椭圆 焦点为F1、F2,双曲线G:x2-y2=4,设P是双曲线G上异于顶点的任一点,直线PF1、PF2与椭圆的交点分别为A、B和C、D.
焦点为F1、F2,双曲线G:x2-y2=4,设P是双曲线G上异于顶点的任一点,直线PF1、PF2与椭圆的交点分别为A、B和C、D.(1)设直线PF1、PF2的斜率分别为k1和k2,求k1•k2的值;
(2)是否存在常数λ,使得|AB|+|CD|=λ|AB|•|CD|恒成立?若存在,试求出λ的值;若不存在,请说明理由.

【答案】分析:(1)设出点P的坐标,表示出斜率,利用P是双曲线G上异于顶点的任一点,即可求得k1•k2的值;
(2)设出直线AB,CD的方程与椭圆方程联立,求得相应弦长,利用|AB|+|CD|=λ|AB|•|CD|,可得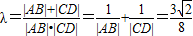 ,从而问题得解.
,从而问题得解.
解答:解:(1)设点P(x,y),x≠±2,那么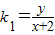 ,
,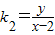
∴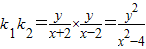
∵P是双曲线G上异于顶点的任一点
∴x2-y2=4,
∴y2=x2-4,
∴k1k2=1
(2)设直线AB:y=k1(x+2),k1≠0
由方程组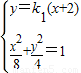 得
得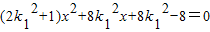
设A(x1,y1),B(x2,y2)
则
由弦长公式得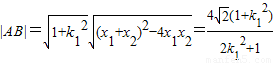
同理设C(x3,y3),D(x4,y4),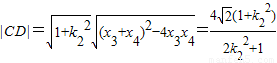
由(1)k1•k2=1得,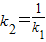 ,代入得
,代入得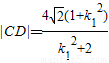
∵|AB|+|CD|=λ|AB|•|CD|,∴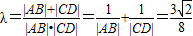
则存在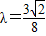 ,使得|AB|+|CD|=λ|AB|•|CD|恒成立.
,使得|AB|+|CD|=λ|AB|•|CD|恒成立.
点评:本题重点考查直线与圆锥曲线的综合,解题的关键是直线与椭圆方程联立,利用弦长公式,综合性强.
(2)设出直线AB,CD的方程与椭圆方程联立,求得相应弦长,利用|AB|+|CD|=λ|AB|•|CD|,可得
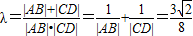 ,从而问题得解.
,从而问题得解.解答:解:(1)设点P(x,y),x≠±2,那么
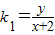 ,
,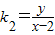
∴
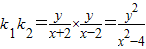
∵P是双曲线G上异于顶点的任一点
∴x2-y2=4,
∴y2=x2-4,
∴k1k2=1
(2)设直线AB:y=k1(x+2),k1≠0
由方程组
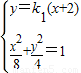 得
得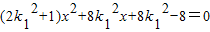
设A(x1,y1),B(x2,y2)
则

由弦长公式得
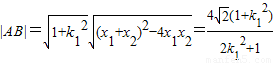
同理设C(x3,y3),D(x4,y4),
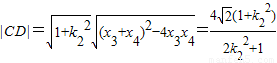
由(1)k1•k2=1得,
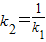 ,代入得
,代入得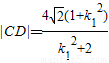
∵|AB|+|CD|=λ|AB|•|CD|,∴
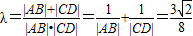
则存在
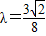 ,使得|AB|+|CD|=λ|AB|•|CD|恒成立.
,使得|AB|+|CD|=λ|AB|•|CD|恒成立.点评:本题重点考查直线与圆锥曲线的综合,解题的关键是直线与椭圆方程联立,利用弦长公式,综合性强.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013•汕头一模)如图.已知椭圆
(2013•汕头一模)如图.已知椭圆 (2013•嘉定区一模)如图,已知椭圆
(2013•嘉定区一模)如图,已知椭圆 焦点为
焦点为 ,双曲线
,双曲线 ,设
,设 是双曲线
是双曲线 上异于顶点的任一点,直线
上异于顶点的任一点,直线 与椭圆的交点分别为
与椭圆的交点分别为 和
和 。
。 和
和 ,求
,求 的值;
的值; ,使得
,使得 恒成立?若存在,试求出
恒成立?若存在,试求出
 分别为其左右焦点,A为左顶点,直线l的方程为x=4,过F2的直线l′与椭圆交于异于A的P、Q两点.
分别为其左右焦点,A为左顶点,直线l的方程为x=4,过F2的直线l′与椭圆交于异于A的P、Q两点. 的取值范围;
的取值范围; 求证:M、N两点的纵坐标之积为定值;并求出该定值.
求证:M、N两点的纵坐标之积为定值;并求出该定值.