题目内容
11. 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.(I)证明:BD⊥平面PAC;
(Ⅱ)若PA=1,AD=2,求点B到平面PCD的距离.
分析 (I)利用线面垂直的性质定理可得PA⊥BD,PC⊥BD,再利用线面垂直的判定定理即可证明.
(II)由于AB∥CD,只要求出点A到平面PCD的距离即可,利用线面面面垂直的判定与性质定理即可得出.
解答 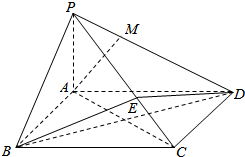 (I)证明:∵PA⊥平面ABCD,∴PA⊥BD,
(I)证明:∵PA⊥平面ABCD,∴PA⊥BD,
∵点E在线段PC上,PC⊥平面BDE.
∴PC⊥BD,又PC∩PA=P,
∴BD⊥平面PAC;
(II)解:∵AB∥CD,AB?平面PCD,CD?平面PCD,
∴AB∥平面 PCD.
∴只要求出点A到平面PCD的距离即可.
过A作AM⊥PD,垂足为M.
∵PA⊥平面ABCD,
∴平面PAD⊥平面ABCD,
∵CD⊥AD,平面PAD∩平面ABCD=AD,
∴CD⊥平面PAD,
∴CD⊥AM,
CD∩PD=D,
∴AM⊥平面ACD,
∵AM=$\frac{PA•AD}{PD}$=$\frac{1×2}{\sqrt{{1}^{2}+{2}^{2}}}$=$\frac{2\sqrt{5}}{5}$.
∴点B到平面PCD的距离是$\frac{2\sqrt{5}}{5}$.
点评 本题考查了空间位置关系及其距离,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
6.如图,在棱长为3的正方体ABCD-A1B1C1D1中,点C1到平面A1BD的距离为( )


| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
16.下列函数中,值域是(0,+∞)的是( )
| A. | y=2x+1(x>1) | B. | y=x2-x+1 | C. | $y=\frac{1}{x}$ | D. | y=$\frac{1}{{x}^{2}}$ |
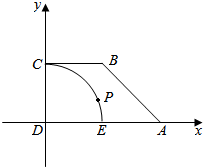 已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=DC=1,以D为圆心,DC为半径,作弧和AD交于点E,点P为劣弧CE上的动点,如图所示.
已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=DC=1,以D为圆心,DC为半径,作弧和AD交于点E,点P为劣弧CE上的动点,如图所示.