题目内容
（1）求log2[log3（log464）]的值；（2）求
的值；（3）解不等式
．
【答案】分析：（1）直接利用对数的运算性质直接求解log2[log3（log464）]的值即可；
（2）直接利用指数的运算性质化简求解
的值；
（3）先利用指数性质转化不等式
为二次不等式，然后求解即可．．
解答：解：（1）log2[log3（log464）]=log2[log3（log443）]=log2[log33]=log21=0；
（2）
=
=22•3-4=
；
（3）不等式
化为．x2-1≥2，即x2≥3，解得x
或x
．
点评：本题考查对数与指数的元素性质的应用，指数不等式的解法，二次不等式的解法，考查计算能力转化思想．
（2）直接利用指数的运算性质化简求解
的值；（3）先利用指数性质转化不等式
为二次不等式，然后求解即可．．解答：解：（1）log2[log3（log464）]=log2[log3（log443）]=log2[log33]=log21=0；
（2）
==22•3-4=；（3）不等式
化为．x2-1≥2，即x2≥3，解得x或x．点评：本题考查对数与指数的元素性质的应用，指数不等式的解法，二次不等式的解法，考查计算能力转化思想．
练习册系列答案
相关题目
A．选修4-1：几何证明选讲
，点P（2，-1）在矩阵A对应的变换下得到点P′（5，1），求矩阵A．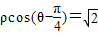
，曲线C的参数方程为
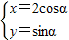（α为参数），求曲线C截直线l所得的弦长．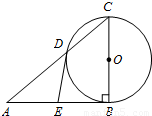
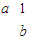）有特征值λ1=2及对应的一个特征向量
．
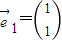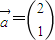，求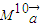
．
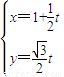（t为参数），曲线C1：
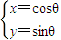（θ为参数）．
倍，纵坐标压缩为原来的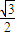
倍，得到曲线C2C，设点P是曲线C2上的一个动点，求它到直线l的距离的最小值．