题目内容
问题：如下图，粗细均匀的玻璃管长L=100厘米，开口向上竖直放置时，上端齐管口有一段h=25厘米的水银柱封闭着27 ℃空气柱，大气压强为p0=75厘米汞柱，如果空气柱温度逐渐升高，欲使管内水银全部溢出，温度至少升到多高？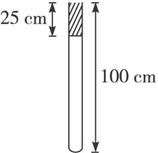
导思：结合物理知识，转化为数学问题，要注意转化的数学式子的特点，寻找可以求最值的方法，而基本不等式的三个要求就是一个特征.
探究：设管内空气柱温度升高到T，管内尚有水银柱x厘米，管的横断面积为S，则有
将数据代入，整理得
T=
由于(75+x)+(100-x)=175为常数，
所以当(75-x)=(100+x)时，即当x=12.5厘米时，T有极大值Tmax=306.25 K.
306.25-273=33.25 ℃.
所以欲使管内水银全部溢出，温度至少升到33.25 ℃.
练习册系列答案
相关题目
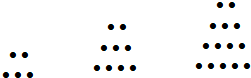两千多年前，古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题．他们在沙滩上画点或用小石子表示数，按照点或小石子能排列的形状对数进行分类．如下图中实心点的个数5，9，14，20，…为梯形数．根据图形的构成，记此数列的第2013项为a2013，则a2013-5=（ ）
