题目内容
已知点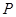 在抛物线
在抛物线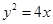 上,那么点
上,那么点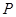 到点
到点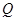 (2,-1)的距离与点
(2,-1)的距离与点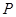 到抛物线焦点距离之和取得最小值时,点
到抛物线焦点距离之和取得最小值时,点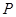 的坐标为( )
的坐标为( )
A.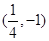 B.
B.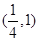 C.
C.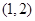 D.
D.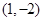
【答案】
A
【解析】
试题分析:已知 (2,-1)在抛物线
(2,-1)在抛物线 内部,而抛物线上的点到焦点的距离等于到准线的距离,所以点
内部,而抛物线上的点到焦点的距离等于到准线的距离,所以点 到点
到点 (2,-1)的距离与点
(2,-1)的距离与点 到抛物线焦点距离之和的最小值为点
到抛物线焦点距离之和的最小值为点 到准线的距离,而抛物线的准线为
到准线的距离,而抛物线的准线为 ,所以点
,所以点 的纵坐标为-1,代入抛物线方程知点P的坐标为
的纵坐标为-1,代入抛物线方程知点P的坐标为 .
.
考点:本小题主要考查抛物线的简单性质.
点评:抛物线上的点最重要的一条性质就是抛物线上的点到焦点的距离等于到准线的距离,所以在求解最值时经常利用这条性质进行转化.

练习册系列答案
相关题目
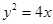 上,那么点P到点Q(2,1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
上,那么点P到点Q(2,1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )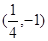 B.
B.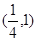 C.
C.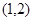 D.
D.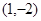
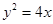 上,那么点P到点Q(2,1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )
上,那么点P到点Q(2,1)的距离与点P到抛物线焦点距离之和取得最小值时,点P的坐标为( )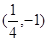 B.
B.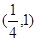 C.
C.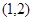 D.
D.