Question

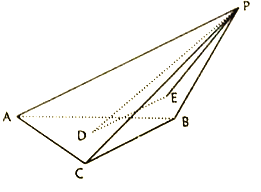
【题目】如图，在三棱锥中， ， ， 为的中点， 为的中点，且为正三角形.

（1）求证： 平面；

（2）若，三棱锥的体积为1，求点到平面的距离.

Answer 1

【答案】（1）见解析;（2）．

【解析】试题分析：

(1)由题意结合几何关系可证得，结合线面垂直的判断定理即可证得平面；

(2)设,结合体积公式计算可得，利用体积相等列方程可得点到平面的距离为．

试题解析：

（1）证明：在正中， 是的中点，所以．

因为是的中点， 是的中点，所以，故．

又， ， 平面，

所以平面．

因为平面，所以．

又平面，

所以平面．

（2）设,则

三棱锥的体积为，得x=2

设点到平面的距离为． 因为为正三角形，所以 ．

因为，所以．

所以．

因为，由（1）知，所以．

在中， ，所以．

因为，

所以，即．

所以．故点到平面的距离为．