题目内容
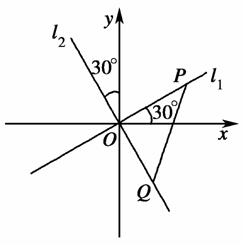
如图,两条过原点O的直线l1,l2分别与x轴、y轴成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.
(1)求动点M(x1,x2)的轨迹C的方程;
(2)设过定点T(0,2)的直线l与(1)中的轨迹C交于不同的两点A、B,且∠AOB为锐角,求直线l的斜率k的取值范围.
[解析] (1)由已知得直线l1⊥l2,
l1y=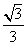 x,l2y=-
x,l2y=-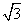 x,
x,
∵点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,
∴y1=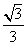 x1,y2=-
x1,y2=-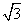 x2,
x2,
由|PQ|=2,得(x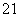 +y
+y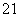 )+(x
)+(x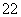 +y
+y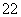 )=4,
)=4,
即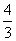 x
x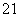 +4x
+4x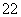 =4⇒
=4⇒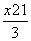 +x
+x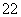 =1,
=1,
∴动点M(x1,x2)的轨迹C的方程为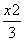 +y2=1.
+y2=1.
(2)直线l的方程为y=kx+2,将其代入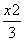 +y2=1,
+y2=1,
化简得(1+3k2)x2+12kx+9=0,
设A(x3,y3)、B(x4,y4),
∴Δ=(12k)2-36×(1+3k2)>0⇒k2>1,
且x3+x4=-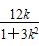 ,x3x4=
,x3x4=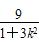 ,
,
∵∠AOB为锐角,∴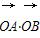 >0,
>0,
即x3x4+y3y4>0⇒x3x4+(kx3+2)(kx4+2)>0,
∴(1+k2)x3x4+2k(x3+x4)+4>0.
将x3+x4=-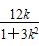 ,x3x4=
,x3x4=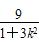 代入上式,
代入上式,
化简得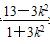 >0⇒k2<
>0⇒k2<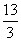 .
.
由k2>1且k2<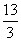 ,得k∈(-
,得k∈(-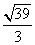 ,-1)∪(1,
,-1)∪(1,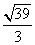 ).
).

练习册系列答案
相关题目
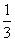 且Sn=n(2n-1)an,通过计算a2,a3,a4,猜想an的表达式是________.
且Sn=n(2n-1)an,通过计算a2,a3,a4,猜想an的表达式是________.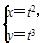 (t为参数)相交于A、B两点,则|AB|=________.
(t为参数)相交于A、B两点,则|AB|=________.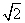 ,在y轴上截得线段长为2
,在y轴上截得线段长为2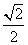 ,求圆P的方程.
,求圆P的方程. =1的左、右焦点,若点P在双曲线上,且
=1的左、右焦点,若点P在双曲线上,且 ·
· =0,则|
=0,则|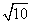 B.2
B.2 D.2
D.2