题目内容
已知函数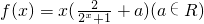 .
.
(1)求实数a使函数f(x)为偶函数?
(2)对于(1)中的a的值,求证:f(x)≤0恒成立.
解:(1)∵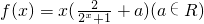 为偶函数
为偶函数
∴f(-x)=f(x)对于任意的x都成立
∴-x(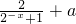 )=x(
)=x(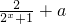 )
)
整理可得,(2+2a)•x=0对于任意x都成立
∴a=-1
(2)证明:当a=-1时,f(x)=x(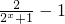 )
)
(i)当x=0时,f(x)=0
(ii)当x>0时,2x+1>2
∴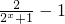 <0
<0
∴f(x)<0
(iii)当x<0时,0<2x+1<2
∴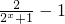 >0
>0
∴f(x)<0
综上可得,f(x)≤0
分析:(1)由题意可得,(-x)=f(x)对于任意的x都成立,代入可求a
(2)证明:当a=-1时,f(x)=x(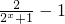 ),分(i)x=0时,f(x)=0,(ii)当x>0时,f(x)<0(iii)当x<0时,f(x)>0,综上可证
),分(i)x=0时,f(x)=0,(ii)当x>0时,f(x)<0(iii)当x<0时,f(x)>0,综上可证
点评:本题主要考查了函数的奇偶性的定义的应用,指数函数的性质在不等式的证明中的应用
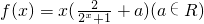 为偶函数
为偶函数∴f(-x)=f(x)对于任意的x都成立
∴-x(
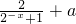 )=x(
)=x(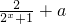 )
)整理可得,(2+2a)•x=0对于任意x都成立
∴a=-1
(2)证明:当a=-1时,f(x)=x(
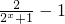 )
)(i)当x=0时,f(x)=0
(ii)当x>0时,2x+1>2
∴
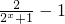 <0
<0∴f(x)<0
(iii)当x<0时,0<2x+1<2
∴
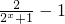 >0
>0∴f(x)<0
综上可得,f(x)≤0
分析:(1)由题意可得,(-x)=f(x)对于任意的x都成立,代入可求a
(2)证明:当a=-1时,f(x)=x(
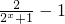 ),分(i)x=0时,f(x)=0,(ii)当x>0时,f(x)<0(iii)当x<0时,f(x)>0,综上可证
),分(i)x=0时,f(x)=0,(ii)当x>0时,f(x)<0(iii)当x<0时,f(x)>0,综上可证点评:本题主要考查了函数的奇偶性的定义的应用,指数函数的性质在不等式的证明中的应用

练习册系列答案
相关题目
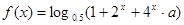 ;
;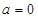 ,求
,求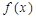 的值域;
的值域;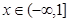 时
时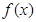 有意义求实
有意义求实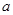 的范围。
的范围。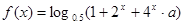 ;
;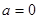 ,求
,求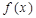 的值域;(2)在(1)的条件下,判断
的值域;(2)在(1)的条件下,判断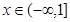 时
时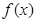 有意义求实
有意义求实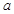 的范围。
的范围。