Question

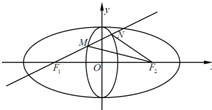（2013•海口二模）定义：若两个椭圆的离心率相等，则称两个椭圆是“相似”的． 如图，椭圆C₁与椭圆C₂是相似的两个椭圆，并且相交于上下两个顶点．椭圆C₁：

x2

a2

+

y2

b2

=1(a＞b＞0)的长轴长是4，椭圆C₂：

y2

m2

+

x2

n2

=1(m＞n＞0)短轴长是1，点F₁，F₂分别是椭圆C₁的左焦点与右焦点，
（Ⅰ）求椭圆C₁，C₂的方程；
（Ⅱ）过F₁的直线交椭圆C₂于点M，N，求△F₂MN面积的最大值．

Answer 1

分析：（Ⅰ）设椭圆C₁的半焦距为c，椭圆C₂的半焦距为c'，易知a=2，b=m，n=

1

2

，根据椭圆C₁与椭圆C₂的离心率相等，可得关于a，b，m，n的方程，解出即可；
（Ⅱ）由题意可设直线的方程为：x=my-

3

．与椭圆C₂的方程联立消掉x得y的二次方程，则△＞0，由弦长公式可表示出|MN|，由点到直线的距离公式可表示出△F₂MN的高h，则△F₂MN的面积S=

1

2

|MN|•h，变形后运用基本不等式即可求得S的最大值；

解答：解：（Ⅰ）设椭圆C₁的半焦距为c，椭圆C₂的半焦距为c'．由已知a=2，b=m，n=

1

2

．
∵椭圆C₁与椭圆C₂的离心率相等，即

c

a

=

c′

m

，
∴

a2-b2

a2

=

m2-n2

m2

，即

1-( b a )2

=

1-( n m )2

∴

b

a

=

n

m

，即bm=b²=an=1，∴b=m=1，
∴椭圆C₁的方程是

x2

4

+y2=1，椭圆C₂的方程是y2+

x2

1 4

=1；
（Ⅱ）显然直线的斜率不为0，故可设直线的方程为：x=my-

3

．
联立：

x=my- 3 y2+4x2=1

，得y2+4(my-

3

)2-1=0，即(1+4m2)y2-8

3

my+11=0，
∴△=192m²-44（1+4m²）=16m²-44＞0，设M（x₁，y₁），N（x₂，y₂），
则y1+y2=

8 3 m

1+4m2

，y1y2=

11

1+4m2

，∴|MN|=2

1+m2

4m2-11

1+4m2

，
△F₂MN的高即为点F₂到直线l：x-my+

3

=0的距离h=

| 3 -0m+ 3 |

1+m2

=

2 3

1+m2

．
∴△F₂MN的面积S=

1

2

|MN|h=2

3

4m2-11

1+4m2

=

2 3

4m2-11 + 12 4m2-11

，
∵

4m2-11

+

12

4m2-11

≥2

12

=4

3

，等号成立当且仅当

4m2-11

=

12

4m2-11

，即m=±

23

2

时，
∴S≤

2 3

4 3

=

1

2

，即△F₂MN的面积的最大值为

1

2

．

点评：本题考查椭圆方程及其性质、直线方程、直线与椭圆的位置关系，考查基本不等式求函数的最值，考查学生的运算能力、分析解决问题的能力．