题目内容
下列函数中,最小值为2 的是
的是
- A.
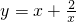
- B.

- C.y=ex+2e-x
- D.y=log2x+2logx2
C
分析:A:当x<0时不能运用基本不等式.
B: 当sinx=
当sinx= 时取到最小值2
时取到最小值2 ,由三角函数的性质可得sinx=
,由三角函数的性质可得sinx= 不成立.
不成立.
C:此函数解析式满足:一正,二定,三相等,所以C正确.
D:当log2x<0时不能运用基本不等式.
解答:A:由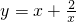 可得:当x<0时不能运用基本不等式,所以A错误.
可得:当x<0时不能运用基本不等式,所以A错误.
B: ≥2
≥2 ,当且仅当sinx=
,当且仅当sinx= 时取等号,由三角函数的性质可得sinx=
时取等号,由三角函数的性质可得sinx= 不成立,所以B错误.
不成立,所以B错误.
C:因为ex>0,所以y=ex+2e-x= ≥2
≥2 ,当且仅当ex=
,当且仅当ex= 时取等号,此函数满足:一正,二定,三相等,所以C正确.
时取等号,此函数满足:一正,二定,三相等,所以C正确.
D:由y=log2x+2logx2可得:当log2x<0时不能运用基本不等式,所以D错误.
故选C.
点评:本题主要考查利用基本不等式求最值,以及三角函数、指数函数、对数函数的有关性质,在利用基本不等式求最值时要满足:一正,二定,三相等,此题属于基础题.
分析:A:当x<0时不能运用基本不等式.
B:
 当sinx=
当sinx= 时取到最小值2
时取到最小值2 ,由三角函数的性质可得sinx=
,由三角函数的性质可得sinx= 不成立.
不成立.C:此函数解析式满足:一正,二定,三相等,所以C正确.
D:当log2x<0时不能运用基本不等式.
解答:A:由
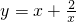 可得:当x<0时不能运用基本不等式,所以A错误.
可得:当x<0时不能运用基本不等式,所以A错误.B:
 ≥2
≥2 ,当且仅当sinx=
,当且仅当sinx= 时取等号,由三角函数的性质可得sinx=
时取等号,由三角函数的性质可得sinx= 不成立,所以B错误.
不成立,所以B错误.C:因为ex>0,所以y=ex+2e-x=
 ≥2
≥2 ,当且仅当ex=
,当且仅当ex= 时取等号,此函数满足:一正,二定,三相等,所以C正确.
时取等号,此函数满足:一正,二定,三相等,所以C正确.D:由y=log2x+2logx2可得:当log2x<0时不能运用基本不等式,所以D错误.
故选C.
点评:本题主要考查利用基本不等式求最值,以及三角函数、指数函数、对数函数的有关性质,在利用基本不等式求最值时要满足:一正,二定,三相等,此题属于基础题.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
下列函数中,最小值为2的是( )
A、y=
| ||||
B、y=lgx+
| ||||
| C、y=3x+3-x,x∈R | ||||
D、y=sin x+
|