Question

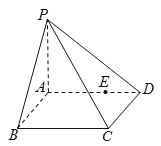
【题目】如图，ABCD是边长为2的正方形，ADPM是梯形，AM∥DP且，，分别为的中点.

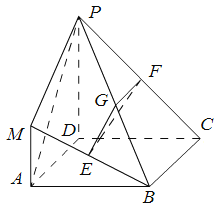
(I)证明：平面;

(II) 求三棱锥的体积。

Answer 1

【答案】(I)见解析(II)

【解析】

(I)先根据条件计算出，得到PD⊥AD, PD⊥CD,

则有CD⊥平面ADPM，即得AB⊥平面ADPM，得到AB⊥EG, 又易得AB⊥FG，得证结论.

(II)先证得AD为点P到平面ABM的距离，再根据体积公式求解.

(I)∵分别为的中点，∴BC∥FG, GE∥MP,

∵ABCD是正方形，∴AB⊥BC, ∴AB⊥FG，可得结论.

∵AD=CD=DP=2,

∴,

∴PD⊥AD, PD⊥CD,

∵AD、CP平面ADPM，AD∩DP=D

∴CD⊥平面ADPM，

∴AB⊥平面ADPM，

∵MP平面ADPM，∴AB⊥MP，

∴AB⊥EG,

∵FG、EG平面EFG，FG∩EG=G

∴平面;

(II)由（I）可知平面ABCD ，

∵,∴平面ABCD，

∴ 又

∴ 平面AMB, ∴AD即为点P到平面ABM的距离，

∵，∴ ，

∴.