题目内容
已知函数 ,其中
,其中 .
.
(Ⅰ)求 最小正周期及对称轴方程;
最小正周期及对称轴方程;
(Ⅱ)在锐角 中,内角
中,内角 的对边分别为
的对边分别为 ,已知
,已知 ,
, ,求
,求 边上的高
边上的高 的最大值.
的最大值.
(Ⅰ) ;
; ;(Ⅱ)
;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)利用二倍角公式,诱导公式和两角和公式对函数解析式进行化简,利用三角函数图象和性质求得其最小正周期T,及对称轴.(Ⅱ)利用三角形面积公式得到h和bc的关系式,进而利用余弦定理得到b和c的关系式,利用基本不等式的性质求得bc的最大值,进而求得h的最大值.
试题解析:(Ⅰ)由题 ,
,
所以f(x)的最小正周期为 ,
,
令 得对称轴方程为
得对称轴方程为 ;
;
(Ⅱ)由题可得
由余弦定理得
即 (当且仅当b=c时取等号)
(当且仅当b=c时取等号)
设BC边上的高为h,由三角形等面积法得

 .
.
即 的最大值为
的最大值为 .
.
考点:三角函数中的恒等变换应用;三角函数的周期性及其求法.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 ,
, ”的否定形式是( )
”的否定形式是( ) ,
, B.
B. ,
,
 ,
, D.
D. ,
,
 }为等差数列,若a
}为等差数列,若a +a
+a =
= ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 ,
, 的最小正周期为
的最小正周期为 ,且
,且 ,则( )
,则( ) ,
, B.
B. ,
,
 ,
, D.
D. ,
,
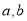 是实数,则“
是实数,则“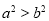 ”是 “
”是 “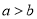 ” 的( )
” 的( ) ,
, ,则
,则 的最小值是 .
的最小值是 . ,则函数
,则函数 的部分图象可以为 ( )
的部分图象可以为 ( )
 的定义域是
的定义域是 ,则函数
,则函数 的定义域是 .
的定义域是 . 是等差数列,若
是等差数列,若  ,则
,则  等于( )
等于( )