题目内容
△ABC的内角为A,B,C,所对的三边分别是a,b,c.若 a,b,c的倒数成等差数列,
(Ⅰ)求证B<
(Ⅱ)若A,B,C也成等差数列,求证△ABC为等边三角形.
(Ⅰ)求证B<
| π | 2 |
(Ⅱ)若A,B,C也成等差数列,求证△ABC为等边三角形.
分析:(I)假设B≥
则b为最大边,有b>a>0,b>c>0,可得
<
+
与已知矛盾.
(II)先确定B的度数,再利用a,b,c的倒数成等差数列,及正弦定理,即可证得结论.
| π |
| 2 |
| 2 |
| b |
| 1 |
| a |
| 1 |
| c |
(II)先确定B的度数,再利用a,b,c的倒数成等差数列,及正弦定理,即可证得结论.
解答:解:(I)假设B≥
则有b>a>0,b>c>0
则
<
,
<
可得
<
+
与已知矛盾,
假设不成立,原命题正确.
(II)∵三内角A、B、C的度数成等差数列
∴2B=A+C,
∵A+B+C=180°,
∴B=60°
设A=60-t,C=60+t.
则
=
+
⇒bc+ba=2ac
⇒sin60°sinC+sin60°sinA=2sinAsinC
⇒sin60°[sin(60°+t)+sin(60°-t)]=2sin(60°+t)sin(60°-t)
⇒
cost=2cos2t-
解得,cost=1,或cost=-
∵t<
,
∴cost=1,t=0°
故A=B=C=60°即△ABC为等边三角形.
| π |
| 2 |
则有b>a>0,b>c>0
则
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
可得
| 2 |
| b |
| 1 |
| a |
| 1 |
| c |
假设不成立,原命题正确.
(II)∵三内角A、B、C的度数成等差数列
∴2B=A+C,
∵A+B+C=180°,
∴B=60°
设A=60-t,C=60+t.
则
| 2 |
| b |
| 1 |
| a |
| 1 |
| c |
⇒sin60°sinC+sin60°sinA=2sinAsinC
⇒sin60°[sin(60°+t)+sin(60°-t)]=2sin(60°+t)sin(60°-t)
⇒
| 3 |
| 2 |
| 1 |
| 2 |
解得,cost=1,或cost=-
| 1 |
| 4 |
∵t<
| π |
| 2 |
∴cost=1,t=0°
故A=B=C=60°即△ABC为等边三角形.
点评:本题考查正弦定理,考查等差数列与等比数列的综合,解题的关键是确定角与边的关系.(I)问使用反证法,比较简单.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
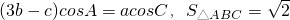 ,则
,则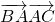 =________.
=________.
 ,则
,则 = .
= .