题目内容
设△ABC的内角为A、B、C所对的边分别为a、b、c,若(3b-c)cosA=acosC,S△ABC=
,则
•
=
| 2 |
| BA |
| AC |
-1
-1
.分析:先利用正弦定理及和角的三角函数,可求cosA的值,进而可求sinA,利用三角形的面积,求得bc.利用向量的数量积公式,即可得到结论.
解答:解:∵(3b-c)cosA=acosC∴由正弦定理,可得:3sinBcosA-sinCcosA=sinAcosC
∴3sinBcosA=sinAcosC+sinCcosA
∴3sinBcosA=sin(A+C)=sinB
∴cosA=
,sinA=
∵S△ABC=
∴
bcsinA=
bc=
∴bc=3
∵cosA=
,
∴cos<
,
>=-
∴
•
=bccos<
,
>=-1
故答案为:-1
∴3sinBcosA=sinAcosC+sinCcosA
∴3sinBcosA=sin(A+C)=sinB
∴cosA=
| 1 |
| 3 |
2
| ||
| 3 |
∵S△ABC=
| 2 |
∴
| 1 |
| 2 |
| ||
| 3 |
| 2 |
∴bc=3
∵cosA=
| 1 |
| 3 |
∴cos<
| BA |
| AC |
| 1 |
| 3 |
∴
| BA |
| AC |
| BA |
| AC |
故答案为:-1
点评:本题考查正弦定理,考查三角形的面积公式,解题的关键是利用正弦定理,进行边角互化.

练习册系列答案
相关题目
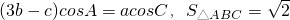 ,则
,则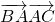 =________.
=________. ,则
,则 = .
= .