题目内容
【题目】已知实数对![]() 满足
满足![]() .
.
(1)求![]() 的最大值和最小值;
的最大值和最小值;
(2)求![]() 的最小值;
的最小值;
(3)求![]() 的最值
的最值
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)整理方程可知,方程表示以点(2,0)为圆心,以![]() 为半径的圆,设
为半径的圆,设![]() ,进而根据圆心(2,0)到
,进而根据圆心(2,0)到![]() 的距离为半径时直线与圆相切,斜率取得最大、最小值;
的距离为半径时直线与圆相切,斜率取得最大、最小值;
(2)设![]() ,仅当直线
,仅当直线![]() 与圆切于第四象限时,纵轴截距
与圆切于第四象限时,纵轴截距![]() 取最小值,进而利用点到直线的距离等于半径求得
取最小值,进而利用点到直线的距离等于半径求得![]() 的最小值;
的最小值;
(3)![]() 是圆上点与原点距离之平方,故连接
是圆上点与原点距离之平方,故连接![]() ,与圆交于B点,并延长交圆于
,与圆交于B点,并延长交圆于![]() ,进而可知
,进而可知![]() 的最大值和最小值分别为
的最大值和最小值分别为![]() 和
和![]() ,答案可得.
,答案可得.
解:(1)方程![]() ,即
,即![]()
表示以点(2,0)为圆心,以![]() 为半径的圆.
为半径的圆.
设![]() ,即
,即![]() ,
,
当圆心(2,0)到![]() 的距离为半径时直线与圆相切,此时斜率分别取得最大、最小值,
的距离为半径时直线与圆相切,此时斜率分别取得最大、最小值,
由![]() ,
,
解得![]() ,
,
所以![]() ;
;

(2)设![]() ,则
,则![]() ,仅当直线
,仅当直线![]() 与圆切于第四象限时,纵轴截距
与圆切于第四象限时,纵轴截距![]() 取最小值.
取最小值.
由点到直线的距离公式,得![]() ,即
,即![]() 或
或![]() ,
,
故![]() ;
;
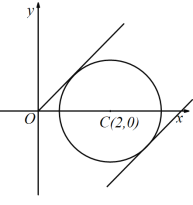
(3)![]() 是圆上点与原点距离之平方,故连接OC,与圆交于B点,并延长交圆于
是圆上点与原点距离之平方,故连接OC,与圆交于B点,并延长交圆于![]() ,可知B到原点的距离最近,点
,可知B到原点的距离最近,点![]() 到原点的距离最大,
到原点的距离最大,
此时有![]() ,
,
则![]() .
.
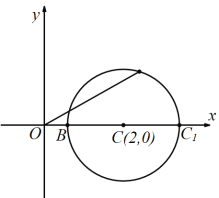

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目

