题目内容
直线x=2与双曲线C：
-y2=1的渐近线交于A，B两点，设P为双曲线C上的任意一点，若
=a
+b
（a，b∈R，O为坐标原点），则下列不等式恒成立的是（ ）
| x2 |
| 4 |
| OP |
| OA |
| OB |
| A．a2+b2≥2 | B．a2+b2≥
| C．a2+b2≤2 | D．a2+b2≤
|
由题意，A（2，1），B（2，-1），
设P（x，y），则∵
=a
+b
∴x=2a+2b，y=a-b
∵P为双曲线C上的任意一点，
∴
-(a-b)2=1
∴4ab=1
∴ab=
∴a2+b2≥2ab=
故选B．
设P（x，y），则∵
| OP |
| OA |
| OB |
∴x=2a+2b，y=a-b
∵P为双曲线C上的任意一点，
∴
| (2a+2b)2 |
| 4 |
∴4ab=1
∴ab=
| 1 |
| 4 |
∴a2+b2≥2ab=
| 1 |
| 2 |
故选B．
练习册系列答案
相关题目
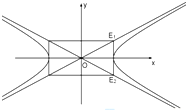如图所示，直线x=2与双曲线C：
的渐近线交于E1，E2两点，记
=
，
=
，任取双曲线C上的点P，若
=a
+b
，则实数a和b满足的一个等式是 ．
的渐近线交于E1，E2两点，记
=
，
=
，任取双曲线C上的点P，若
=a
+b
，则实数a和b满足的一个等式是 ．