题目内容
若不共线的非零向量
，
满足(
+
)•(
-
)=0，且|
-
|=|
|，则向量
-
与
的夹角是
．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| π |
| 3 |
| π |
| 3 |
分析：利用(
+
)•(
-
)=0，可得|
|=|
|，利用|
-
|=|
|，可得
•
=
2，利用向量的夹角公式，即可求得结论．
| a |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
| a |
| a |
| b |
| 1 |
| 2 |
| b |
解答：解：∵(
+
)•(
-
)=0，∴
2-
2=0，
∴|
|=|
|
∵|
-
|=|
|，∴
2-2
•
+
2=
2
∴
•
=
2
设向量
-
与
的夹角是α，则cosα=
=
=
∵α∈[0，π]，∴α=
故答案为：
| a |
| b |
| a |
| b |
| a |
| b |
∴|
| b |
| a |
∵|
| a |
| b |
| a |
| a |
| a |
| b |
| b |
| a |
∴
| a |
| b |
| 1 |
| 2 |
| b |
设向量
| a |
| b |
| a |
(
| ||||||
|
|
| ||||
|
| 1 |
| 2 |
∵α∈[0，π]，∴α=
| π |
| 3 |
故答案为：
| π |
| 3 |
点评：本题考查向量知识的运用，考查向量的数量积公式，考查学生的计算能力，属于中档题．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
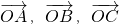满足
，三点A，B，C共线且该直线不过O点，则S2010等于________．
满足
，三点A，B，C共线且该直线不过O点，则S2010等于 ．