题目内容
直线l交抛物线y2=2x于M(x1,y1),N(x2,y2),且 l过焦点,则y1y2的值为
-1
-1
.分析:先确定抛物线的焦点坐标,再设直线方程代入抛物线方程,利用韦达定理可求.
解答:解:由题意,抛物线的焦点坐标为(
,0),
设直线l为x=my+
,代入抛物线方程得y2-2my-1=0
∵直线l交抛物线y2=2x于M(x1,y1),N(x2,y2),
∴y1y2=-1
故答案为-1
| 1 |
| 2 |
设直线l为x=my+
| 1 |
| 2 |
∵直线l交抛物线y2=2x于M(x1,y1),N(x2,y2),
∴y1y2=-1
故答案为-1
点评:本题以抛物线为载体,考查直线与抛物线的位置关系,关键是求出抛物线的焦点坐标.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
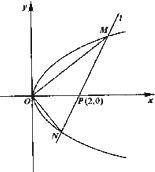 如图,O为坐标原点,过点P(2,0)且斜率为k的直线l交抛物线y2=2x于M(x1,y1),N(x2,y2)两点.
如图,O为坐标原点,过点P(2,0)且斜率为k的直线l交抛物线y2=2x于M(x1,y1),N(x2,y2)两点. 如图,在直角坐标系xOy中,过点P(2,0)的直线l交抛物线y2=2x于M(x1,y1),N(x2,y2)两点.
如图,在直角坐标系xOy中,过点P(2,0)的直线l交抛物线y2=2x于M(x1,y1),N(x2,y2)两点.