题目内容
甲、乙、丙三人进行乒乓球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判.设各局中双方获胜的概率均为 ,各局比赛的结果相互独立,第1局甲当裁判.
,各局比赛的结果相互独立,第1局甲当裁判.
(Ⅰ)求第4局甲当裁判的概率;
(Ⅱ)用X表示前4局中乙当裁判的次数,求X的分布列和数学期望.
解:(Ⅰ)记A1表示事件“第2局结果为甲胜”,
A2表示事件“第3局甲参加比赛时,结果为甲负”,
A表示事件“第4局甲当裁判”.
则A=A1·A2.
P(A)=P(A1·A2)=P(A1)P(A2)= .
.
(Ⅱ)X的可能取值为0,1,2.
记A3表示事件“第3局乙和丙比赛时,结果为乙胜丙”,
B1表示事件“第1局结果为乙胜丙”,
B2表示事件“第2局乙和甲比赛时,结果为乙胜甲”,
B3表示事件“第3局乙参加比赛时,结果为乙负”.
则P(X=0)=P(B1·B2·A3)=P(B1)P(B2)P(A3)= ,
,
P(X=2)=P( ·B3)=P(
·B3)=P( )P(B3)=
)P(B3)= ,
,
P(X=1)=1-P(X=0)-P(X=2)=1- -
- =
= .
.
∴X的分布列为
| X | 0 | 1 | 2 |
| P |
|
|
|

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 轴上,左、右焦点分别为
轴上,左、右焦点分别为 ,且它们在第一象限的交点为
,且它们在第一象限的交点为 ,
, 是以
是以 为底边的等腰三角形,若双曲线的离心率的取值范围为
为底边的等腰三角形,若双曲线的离心率的取值范围为 .则该椭圆的离心率的取值范围是 .
.则该椭圆的离心率的取值范围是 . 的解集是 .
的解集是 .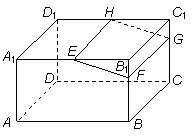 如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a.在长方体ABCD-A1B1C1D1内随机选取一点,记该点取自于几何体A1ABFE-D1DCGH内的概率为P,当点E,F分别在棱A1B1,BB1上运动且满足EF=a时,则P的最小值为
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a.在长方体ABCD-A1B1C1D1内随机选取一点,记该点取自于几何体A1ABFE-D1DCGH内的概率为P,当点E,F分别在棱A1B1,BB1上运动且满足EF=a时,则P的最小值为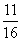 B.
B.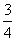 C.
C.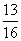 D.
D.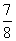
 =
= ,DE交AB于点F.若AB=4,BP=3,则PF= .
,DE交AB于点F.若AB=4,BP=3,则PF= .
 的图象向左平移
的图象向左平移 个单位,若所得图象与原图象重合,则
个单位,若所得图象与原图象重合,则 的值不可能等于( )
的值不可能等于( )
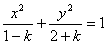 的焦点在x轴上,则k的取值范围为 .
的焦点在x轴上,则k的取值范围为 .