Question

【题目】如图，已知矩形 所在平面与等腰直角三角形 所在平面互相垂直， ， ， 为线段 的中点．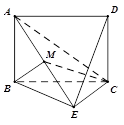
（Ⅰ）证明： ；
（Ⅱ）求 与平面 所成的角的余弦值．

Answer 1

【答案】解：（Ⅰ） 因为 ，所以 ，故 ．因为 ，所以 ，故 ．
因为 ， 为 的中点，所以 ．
所以 ．
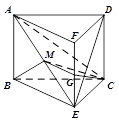
（Ⅱ）如图，将几何体 补成三棱柱 ，

设 的中点为 ，连结 ．
因为 ，所以 ．
因此 为 与平面 所成的角．
不妨设 ，则 ，因此 ， ， ，故 ，
所以 与平面 所成的角的余弦值为 ．
【解析】（Ⅰ）由已知推导出AB⊥EC，EC⊥BM，AE⊥BM，由此能证明BM⊥平面AEC．
（Ⅱ）将几何体ABCDE补成三棱柱AFD-BEC，设EF的中点为G，连结MG，GC，推导出∠MCG为MC与平面DEC所成的角，由此能求出MC与平面DEC所成的角的余弦值．
【考点精析】掌握直线与平面垂直的判定是解答本题的根本，需要知道一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．