Question

△ABC中，∠C=90°，∠B=30°，AC=2，M是AB的中点．将△ACM沿CM折起，使A，B两点间的距离为 2

2

，此时三棱锥A-BCM的体积等于______．

Answer 1

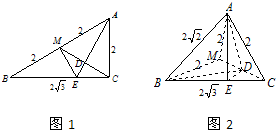
由已知得AB=4，AM=MB=MC=2，BC=2

3

，
由△AMC为等边三角形，取CM中点，则AD⊥CM，AD交BC于E，则AD=

3

，DE=

3

3

，
CE=

2 3

3

．
折起后，由BC²=AC²+AB²，知∠BAC=90°，
又cos∠ECA=

3

3

．∴AE²=CA²+CE²-2CA•CEcos∠ECA=

8

3

，于是AC²=AE²+CE²．?∠AEC=90°．
∵AD²=AE²+ED²，?AE⊥平面BCM，即AE是三棱锥A-BCM的高，AE=

2 6

3

．
∴S_△BCM=

3

，
V_A-BCM=

2 2

3

．
故答案为

2 2

3

．