题目内容
在平面直角坐标系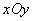 中,已知抛物线
中,已知抛物线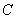 :
: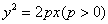 ,在此抛物线上一点
,在此抛物线上一点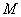
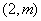 到焦点的距离是3.
到焦点的距离是3.
(1)求此抛物线的方程;
(2)抛物线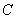 的准线与
的准线与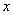 轴交于
轴交于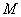 点,过
点,过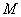 点斜率为
点斜率为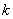 的直线
的直线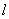 与抛物线
与抛物线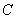 交于
交于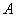 、
、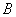 两点.是否存在这样的
两点.是否存在这样的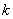 ,使得抛物线
,使得抛物线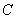 上总存在点
上总存在点 满足
满足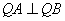 ,若存在,求
,若存在,求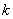 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
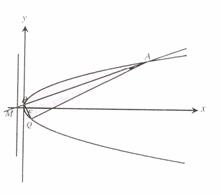
解:(1)抛物线准线方程是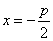 ,
,
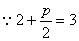 ,
,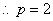
∴抛物线的方程是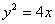
(2)设 ,
,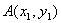 ,
,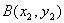
由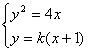 得
得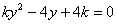 ,
,
由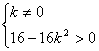 得
得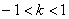 且
且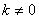 .
.
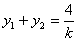 ,
,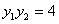
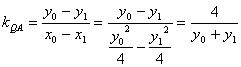 ,同理
,同理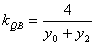
由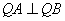 得
得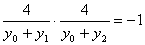 ,
,
即: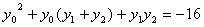 ,
,
∴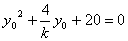 , .
, .
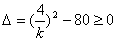 ,得
,得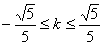 且
且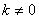 ,
,
由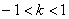 且
且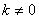 得,
得,
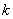 的取值范围为
的取值范围为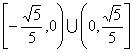

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
观察两相关变量得如下数据:
| x | -9 | -6.99 | -5.01 | -3 |
| y | -9 | -7 | -5 | -3 |
| -5 | 5 | 4 | 4 |
| -4.01 | -4.99 | 5.01 | 3.99 |
则这两变量间的回归直线方程为( )
A.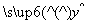 =
=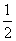 x+1 B.
x+1 B.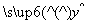 =x C.
=x C.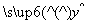 =2x+
=2x+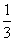 D.
D.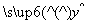 =x+1
=x+1
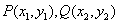 之间的“直角距离”为
之间的“直角距离”为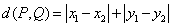
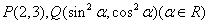 ,则
,则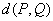 为定值;
为定值; 到直线
到直线 上任一点P的直角距离
上任一点P的直角距离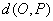 的最小值为
的最小值为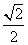 ;与
;与 表示
表示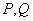 两点间的距离,那么
两点间的距离,那么 ;
; 且
且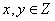 ,若点
,若点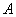 在过点
在过点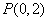 与
与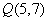 的直线上,且点
的直线上,且点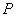 与
与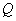 的“直角距离”之和等于10,那么满足条件的点A只有5个。
的“直角距离”之和等于10,那么满足条件的点A只有5个。 与
与 互相垂直,则点
互相垂直,则点 到
到 轴的距离为 .
轴的距离为 .  相外切,且与定直线L:
相外切,且与定直线L: 相切,则此动圆的圆心M的轨迹方程是( )
相切,则此动圆的圆心M的轨迹方程是( ) B.
B. C.
C. D.
D.
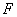 上,且灯的深度
上,且灯的深度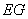 等于灯口直径
等于灯口直径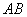 ,且为64
,且为64 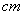 ,则光源安装的位置
,则光源安装的位置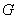 的距离为____________
的距离为____________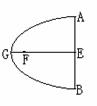

 的夹角为
的夹角为 ,
, ,则
,则


 及直线
及直线 截圆C所得的弦长均为8,则圆C的面积是 .
截圆C所得的弦长均为8,则圆C的面积是 . D.
D.