题目内容
给定向量 且满足
且满足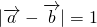 ,若对任意向量
,若对任意向量 满足
满足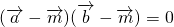 ,则
,则 的最大值与最小值之差为
的最大值与最小值之差为
- A.2
- B.1
- C.

- D.

B
分析:令 =
= 可得
可得  ⊥
⊥ ,有|
,有| +
+ |=|
|=| -
- |=1,当
|=1,当  ≠
≠ 时,把
时,把 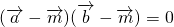 展开化简可得|
展开化简可得| |=1,故
|=1,故 的最大值为1,最小值为0.
的最大值为1,最小值为0.
解答:∵对任意向量 满足
满足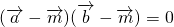 ,∴当
,∴当  =
= 时,
时, •
• =0,故
=0,故  ⊥
⊥ .
.
∵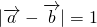 ,由向量加减法的几何意义得|
,由向量加减法的几何意义得| +
+ |=1.
|=1.
由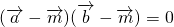 可得,
可得, •
• -
- •(
•( +
+ )+
)+ =0,∴
=0,∴ =
= •(
•( +
+ ),
),
∴ =|
=| |•|
|•| +
+ |=|
|=| |,∴|
|,∴| |=1,
|=1,
又∵| |≥0,故
|≥0,故 的最大值与最小值之差为 1-0=1,
的最大值与最小值之差为 1-0=1,
故选 B.
点评:本题考查向量的模的定义,向量加减法的几何意义,两个向量垂直的条件.
分析:令
 =
= 可得
可得  ⊥
⊥ ,有|
,有| +
+ |=|
|=| -
- |=1,当
|=1,当  ≠
≠ 时,把
时,把 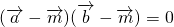 展开化简可得|
展开化简可得| |=1,故
|=1,故 的最大值为1,最小值为0.
的最大值为1,最小值为0.解答:∵对任意向量
 满足
满足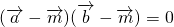 ,∴当
,∴当  =
= 时,
时, •
• =0,故
=0,故  ⊥
⊥ .
.∵
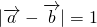 ,由向量加减法的几何意义得|
,由向量加减法的几何意义得| +
+ |=1.
|=1.由
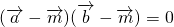 可得,
可得, •
• -
- •(
•( +
+ )+
)+ =0,∴
=0,∴ =
= •(
•( +
+ ),
),∴
 =|
=| |•|
|•| +
+ |=|
|=| |,∴|
|,∴| |=1,
|=1,又∵|
 |≥0,故
|≥0,故 的最大值与最小值之差为 1-0=1,
的最大值与最小值之差为 1-0=1,故选 B.
点评:本题考查向量的模的定义,向量加减法的几何意义,两个向量垂直的条件.

练习册系列答案
相关题目
给定向量
,
且满足|
-
|=1,若对任意向量
满足(
-
)•(
-
)=0,则|
|的最大值与最小值之差为( )
| a |
| b |
| a |
| b |
| m |
| a |
| m |
| b |
| m |
| m |
| A、2 | ||||
| B、1 | ||||
C、
| ||||
D、
|
 且满足
且满足 ,若对任意向量
,若对任意向量 满足
满足 ,则
,则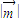 的最大值与最小值之差为( )
的最大值与最小值之差为( )
