��Ŀ����
��֪��ԲC��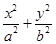 ��1(a>b>0)����������F1��F2��������������B1��B2��һ���߳�Ϊ2�ҡ�F1B1F2Ϊ60������ε��ĸ����㣮
��1(a>b>0)����������F1��F2��������������B1��B2��һ���߳�Ϊ2�ҡ�F1B1F2Ϊ60������ε��ĸ����㣮
(1)����ԲC�ķ��̣�
(2)���ҽ���F2��б��Ϊk(k��0)��ֱ��l����ԲC�ཻ��E��F���㣬AΪ��Բ���Ҷ��㣬ֱ��AE��AF�ֱ�ֱ��x��3�ڵ�M��N���߶�MN���е�ΪP����ֱ��PF2��б��Ϊk�䣬��֤�� k��k��Ϊ��ֵ��
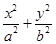 ��1(a>b>0)����������F1��F2��������������B1��B2��һ���߳�Ϊ2�ҡ�F1B1F2Ϊ60������ε��ĸ����㣮
��1(a>b>0)����������F1��F2��������������B1��B2��һ���߳�Ϊ2�ҡ�F1B1F2Ϊ60������ε��ĸ����㣮(1)����ԲC�ķ��̣�
(2)���ҽ���F2��б��Ϊk(k��0)��ֱ��l����ԲC�ཻ��E��F���㣬AΪ��Բ���Ҷ��㣬ֱ��AE��AF�ֱ�ֱ��x��3�ڵ�M��N���߶�MN���е�ΪP����ֱ��PF2��б��Ϊk�䣬��֤�� k��k��Ϊ��ֵ��
��1�� ��1��2����
��1��2����
 ��1��2����
��1��2����
(1)�⡡������֪a��2��b�� ����������Բ����Ϊ
����������Բ����Ϊ ��1.
��1.
(2)֤���������F2(1,0)��ֱ��l����Ϊ��y��k(x��1)�����E(x1��y1)����F(x2��y2)����ֱ��l����y��k(x��1)������ԲC�ķ��� ��1�������ã�(4k2��3)x2��8k2x��4k2��12��0����Ϊ��F2����Բ�ڣ�����ֱ��l����Բ�ཻ����>0���������x1��x2��
��1�������ã�(4k2��3)x2��8k2x��4k2��12��0����Ϊ��F2����Բ�ڣ�����ֱ��l����Բ�ཻ����>0���������x1��x2�� ��x1x2��
��x1x2�� .
.
ֱ��AE�ķ���Ϊ��y�� (x��2)��ֱ��AF�ķ���Ϊ��y��
(x��2)��ֱ��AF�ķ���Ϊ��y�� (x��2)����x��3�õ�M
(x��2)����x��3�õ�M ��N
��N �����P����Ϊ
�����P����Ϊ ��
��
ֱ��PF2��б��Ϊk�䣽 ��
�� ��
�� ��
�� .
.
��x1��x2�� ��x1x2��
��x1x2�� ������ʽ�ã�
������ʽ�ã�
k�䣽 ��
�� .
.
����k��k��Ϊ��ֵ�� .
.
 ����������Բ����Ϊ
����������Բ����Ϊ ��1.
��1.(2)֤���������F2(1,0)��ֱ��l����Ϊ��y��k(x��1)�����E(x1��y1)����F(x2��y2)����ֱ��l����y��k(x��1)������ԲC�ķ���
 ��1�������ã�(4k2��3)x2��8k2x��4k2��12��0����Ϊ��F2����Բ�ڣ�����ֱ��l����Բ�ཻ����>0���������x1��x2��
��1�������ã�(4k2��3)x2��8k2x��4k2��12��0����Ϊ��F2����Բ�ڣ�����ֱ��l����Բ�ཻ����>0���������x1��x2�� ��x1x2��
��x1x2�� .
.ֱ��AE�ķ���Ϊ��y��
 (x��2)��ֱ��AF�ķ���Ϊ��y��
(x��2)��ֱ��AF�ķ���Ϊ��y�� (x��2)����x��3�õ�M
(x��2)����x��3�õ�M ��N
��N �����P����Ϊ
�����P����Ϊ ��
��ֱ��PF2��б��Ϊk�䣽
 ��
�� ��
�� ��
�� .
.��x1��x2��
 ��x1x2��
��x1x2�� ������ʽ�ã�
������ʽ�ã�k�䣽
 ��
�� .
.����k��k��Ϊ��ֵ��
 .
.
��ϰ��ϵ�д�
 ʱ�����������ҵԭ���ܳ�����ϵ�д�
ʱ�����������ҵԭ���ܳ�����ϵ�д� ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�
�����Ŀ
��֪�� ��
�� ������
������ ���㣺
���㣺 ����
����
��1���� �Ĺ켣
�Ĺ켣 �ķ��̣�
�ķ��̣�
��2����֪ԲW�� ������
������ ��켣
��켣 �ཻ��P��Q���㣬��֤����PQΪֱ����Բ��������ԭ��
�ཻ��P��Q���㣬��֤����PQΪֱ����Բ��������ԭ�� .
.
 ��
�� ������
������ ���㣺
���㣺 ����
����
��1����
 �Ĺ켣
�Ĺ켣 �ķ��̣�
�ķ��̣���2����֪ԲW��
 ������
������ ��켣
��켣 �ཻ��P��Q���㣬��֤����PQΪֱ����Բ��������ԭ��
�ཻ��P��Q���㣬��֤����PQΪֱ����Բ��������ԭ�� .
.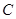 �ķ���Ϊ
�ķ���Ϊ ����������
����������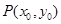 (
(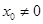 )��б��Ϊ
)��б��Ϊ ������ֱ�߷ֱ�������
������ֱ�߷ֱ�������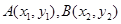 ����(
����(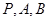 ���㻥����ͬ)��������
���㻥����ͬ)��������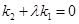 ��
��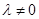 ��
��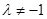 ����
����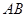 ��һ��
��һ��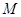 ������
������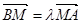 ��֤���߶�
��֤���߶�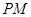 ���е���
���е���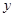 ���ϣ�
���ϣ� =1ʱ������
=1ʱ������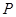 ������Ϊ
������Ϊ ����
���� Ϊ�۽�ʱ��
Ϊ�۽�ʱ�� ��������
��������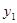 ��ȡֵ��Χ.
��ȡֵ��Χ.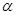 ��ֱ��m��˫������M��N���㣬����
��ֱ��m��˫������M��N���㣬����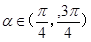 ��F2��˫���ߵ��ҽ��㣬���F2MN�����S������б��
��F2��˫���ߵ��ҽ��㣬���F2MN�����S������б��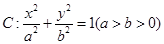 ��������������ֱ�Ϊ
��������������ֱ�Ϊ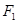 ��
�� ���϶���
���϶��� ��
��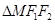 Ϊ�����������ܳ�Ϊ6��ֱ��
Ϊ�����������ܳ�Ϊ6��ֱ�� ����Բ
����Բ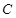 �ཻ��
�ཻ�� ����.
����.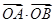 ��ȡֵ��Χ.
��ȡֵ��Χ.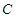 �Ķ���������ԭ��
�Ķ���������ԭ��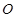 ���Գ���Ϊ
���Գ���Ϊ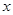 �ᣬ����Ϊ
�ᣬ����Ϊ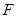 ,��������һ��
,��������һ��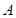 �ĺ�����Ϊ2����
�ĺ�����Ϊ2����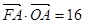 .
.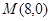 ��ֱ��
��ֱ��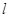 ����������
����������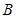 ��
��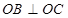 .
.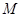 ��
��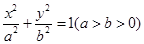 ��������������е������㣺
��������������е������㣺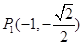 ��
��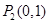 ��
��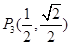 ��
��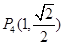 ��
��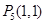 .
.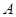 Ϊ��Բ
Ϊ��Բ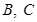 Ϊ��Բ
Ϊ��Բ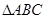 ���ⲿ����
���ⲿ����