题目内容
已知双曲线x2-y2=2若直线n的斜率为2 ,直线n与双曲线相交于A、B两点,线段AB的中点为P,
(1)求点P的坐标(x,y)满足的方程(不要求写出变量的取值范围);
(2)过双曲线的左焦点F1,作倾斜角为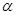 的直线m交双曲线于M、N两点,期中
的直线m交双曲线于M、N两点,期中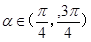 ,F2是双曲线的右焦点,求△F2MN的面积S关于倾斜角
,F2是双曲线的右焦点,求△F2MN的面积S关于倾斜角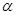 的表达式。
的表达式。
(1)求点P的坐标(x,y)满足的方程(不要求写出变量的取值范围);
(2)过双曲线的左焦点F1,作倾斜角为
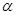 的直线m交双曲线于M、N两点,期中
的直线m交双曲线于M、N两点,期中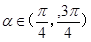 ,F2是双曲线的右焦点,求△F2MN的面积S关于倾斜角
,F2是双曲线的右焦点,求△F2MN的面积S关于倾斜角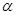 的表达式。
的表达式。(1) (可以写出范围:
(可以写出范围: 或
或 ),不写也不扣分);
),不写也不扣分);
(2)
 (可以写出范围:
(可以写出范围: 或
或 ),不写也不扣分);
),不写也不扣分);(2)

试题分析:(1) 这类问题基本方法是设直线方程为
 ,代入双曲线方程化简后可得
,代入双曲线方程化简后可得 ,同时设中点
,同时设中点 坐标为
坐标为 ,则有
,则有 ,又
,又 ,即
,即 ,再代入
,再代入 即得出所求中点轨迹方程;对于求圆锥曲线中点轨迹方程,我们还可以采取设而不求的方法,即设
即得出所求中点轨迹方程;对于求圆锥曲线中点轨迹方程,我们还可以采取设而不求的方法,即设 ,中点
,中点 ,只要把
,只要把 两点坐标代入圆锥曲线方程,所得两式相减,即可得出
两点坐标代入圆锥曲线方程,所得两式相减,即可得出 与
与 的关系,前者是直线
的关系,前者是直线 的斜率,后者正是
的斜率,后者正是 点坐标的关系
点坐标的关系 ,由此可很快得到所求轨迹方程;(2) 设
,由此可很快得到所求轨迹方程;(2) 设 ,
, ,由于
,由于 ,因此
,因此 ,而
,而 可以用直线
可以用直线 方程与双曲线方程联立方程组,消去
方程与双曲线方程联立方程组,消去 可得
可得 的一元二次方程,从这个方程可得
的一元二次方程,从这个方程可得 ,从而得三角形面积,但要注意当直线
,从而得三角形面积,但要注意当直线 斜率不存在时需另外求.
斜率不存在时需另外求.试题解析:(1)解法1:设直线
 方程为
方程为 ,
,代入双曲线方程得:
 , 2分
, 2分由
 得
得 .设
.设 、
、 两点坐标分别为
两点坐标分别为 、
、 ,则有
,则有 ;又由韦达定理知:
;又由韦达定理知: , 4分
, 4分所以
 ,即得点
,即得点 的坐标
的坐标 所满足的方程
所满足的方程 . 5分
. 5分注:
 或
或 ,点
,点 的轨迹为两条不包括端点的射线.
的轨迹为两条不包括端点的射线.解法2:设
 、
、 两点坐标分别为
两点坐标分别为 、
、 ,则有
,则有 ,
, ,两式相减得:
,两式相减得: (*). 2分
(*). 2分又因为直线
 的斜率为2,所以
的斜率为2,所以 ,再由线段
,再由线段 中点
中点 的坐标
的坐标 ,得
,得 . 4分
. 4分代入(*)式即得点
 的坐标
的坐标 所满足的方程
所满足的方程 . 5分
. 5分(2)
 ,
, ,直线
,直线 与
与 轴垂直时,
轴垂直时, ,此时,△
,此时,△ 的面积
的面积 =
= . 6分
. 6分直线
 与
与 轴不垂直时,直线
轴不垂直时,直线 方程为
方程为 , 7分
, 7分设
 ,
,解法1:将
 代入双曲线,整理得:
代入双曲线,整理得: ,即
,即 9分
9分所以,
 10分
10分
 =
= . 13分
. 13分所以,
 . 14分
. 14分解法2:参见理科解法2。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
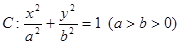 的右焦点为
的右焦点为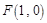 ,设左顶点为A,上顶点为B且
,设左顶点为A,上顶点为B且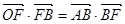 ,如图.
,如图.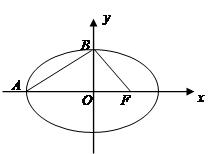
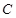 的方程;
的方程;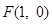 ,过
,过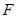 的直线
的直线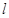 交椭圆于
交椭圆于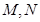 两点,试确定
两点,试确定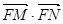 的取值范围.
的取值范围.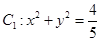 ,直线
,直线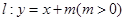 与圆
与圆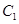 相切,且交椭圆
相切,且交椭圆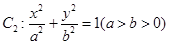 于
于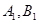 两点,c是椭圆的半焦距,
两点,c是椭圆的半焦距, .
.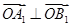 ,求椭圆
,求椭圆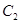 的方程;
的方程;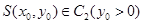 ,直线
,直线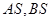 与直线
与直线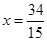 分别交于M,N两点,求线段MN的长度的最小值.
分别交于M,N两点,求线段MN的长度的最小值.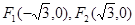 ,曲线C是使
,曲线C是使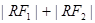 为定值的点
为定值的点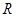 的轨迹,曲线
的轨迹,曲线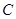 过点
过点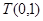 .
.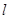 过点
过点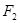 ,且与曲线
,且与曲线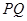 ,当
,当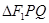 的面积取得最大值时,求直线
的面积取得最大值时,求直线 是曲线
是曲线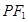 、
、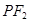 ,设
,设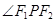 的角平分线
的角平分线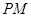 交曲线
交曲线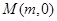 ,求
,求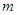 的取值范围.
的取值范围.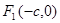 、
、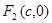 分别是椭圆
分别是椭圆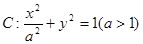 的左、右焦点,
的左、右焦点,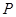 为椭圆
为椭圆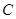 上任意一点,且
上任意一点,且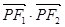 的最小值为
的最小值为 .
.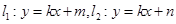 (直线
(直线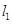 、
、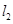 不重合),若
不重合),若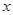 轴上是否存在定点
轴上是否存在定点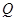 ,使点
,使点 +
+ =1(a>b>0),左、右两个焦点分别为F1,F2,上顶点A(0,b),△AF1F2为正三角形且周长为6.
=1(a>b>0),左、右两个焦点分别为F1,F2,上顶点A(0,b),△AF1F2为正三角形且周长为6.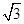 ,1)到两焦点的距离之和为4
,1)到两焦点的距离之和为4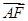 =3
=3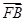 .求过O,A,B三点的圆的方程.
.求过O,A,B三点的圆的方程.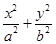 =1(a>b>0)的两个焦点F1,F2和上下两个顶点B1,B2是一个边长为2且∠F1B1F2为60°的菱形的四个顶点.
=1(a>b>0)的两个焦点F1,F2和上下两个顶点B1,B2是一个边长为2且∠F1B1F2为60°的菱形的四个顶点. 到两个定点
到两个定点 的距离之差的绝对值等于8,则动点M的轨迹方程为 ( )
的距离之差的绝对值等于8,则动点M的轨迹方程为 ( )


